|
| ||||||
|
| ||||||||
|
| ||||||||
Home  Publications Publications |
|
|
Genetic Analysis of Variation in Neuron Number Richelle Cutler Strom Chapter 3: Mapping Genes Controlling Brain Weight Variation Using Recombinant Inbred strains and F2 Intercross Progeny Introduction The high heritability of brain weight together with the estimate of a relatively small number of genes affecting this trait, indicate that it should be possible to map at least several responsible for variation in brain weight. In this study, I map quantitative trait loci that are responsible for variation in brain weight between mouse strains using the recombinant inbred (RI) strains, BXD and AXB/BXA, and an F2 intercross. Belknap and colleagues (1992) used the BXD RI strains to map QTLs responsible for brain weight differences between DBA/2J and C57BL/6J (Belknap, 1992). In the Belknap study, only 20 RI strains were used, whereas my BXD analysis includes 26 strains. Also, Belknap’s study uses 360 markers, whereas I use a data set that includes 529 markers. The increase in both strain number and marker density greatly improves the power of detecting significant associations. In addition, this study combines two sets of RI strains and an F2 intercross for the purpose of QTL confirmation. The same genetic interval could be linked to variation in brain weight in more than one cross. Identifying the same QTLs is especially likely in this study since there are some common parental origins between the crosses, ABXD5F2, AXB/BXA, and BXD. For example, ABXD5F2 share the A/J parental with the AXB/BXA RI strains, DBA/2J is a parental for the BXD strains, including BXD5, which is a parental in ABXD5F2. In addition, all of the crosses have C57BL/6J origins in common. The detection of the same linkage interval in multiple crosses will provide QTL verification. I also expect to identify unique QTLs within each cross since there will be different allele segregating between the crosses. There are several advantages in using RI strains for QTL analysis. First, since the individuals of each RI strain are isogenic an infinite number of mice can be phenotyped to obtain a strain average. Obtaining a strain average serves to reduce the environmental and technical variance, that can obscure the association between a phenotype and a genotype. Second, with RI strains there is no genotyping necessary since there are hundreds of marker loci already typed for each RI strain. Another advantage with RI strains is that during the generation of each RI strain, there were multiple opportunities for recombination, resulting in a 4-fold increase in resolving power for determining linkage distance. The F2 intercross has the advantage of being able to detect genes with a lower effect size, which are not detected in an RI analysis due to the limited number of strains in a set (Johnson et al., 1992). However, detecting and positioning QTLs with reasonable accuracy requires genotyping and phenotyping a large number of intercross progeny. The number of progeny necessary to genotype can be reduced by first phenotyping and then selecting the animals from the phenotypic extremes for genotyping (Darvasi, 1997; Lander and Botstein, 1989). This technique is called selective genotyping and in addition to saving time, the progeny with phenotypic extremes will have parental genotypes, which are the most informative for linkage detection (Tanksley, 1993). Materials and methods The BXD set consisted of 26 strains that were generated from parental strains, DBA/2J and C57BL/6J, which have a 73 mg difference in brain weight. All the BXD mice were obtained directly from the Jackson Laboratory (Bar Harbor, ME). The AXB, BXA RI strains were produced from reciprocal crosses between the inbred strains A/J and C57BL/6J. The strains A/J and C57BL/6J have an 80 mg difference in brain weight. Brain weights were obtained for 24 AXB/BXA strains. Mating pairs for each of the 24 AXB/BXA RI strains were obtained from the Jackson Laboratory and the majority of the mice were generated in the mouse colony at the University of Tennessee. The ABXD5F2 progeny were generated from a cross between A/J and BXD5 (n = 542). The strains A/J and BXD5 have a 106 mg difference in brain weight. The BXD5 strain has one of the heaviest brain weights of all inbred strains—528 mg, while A/J has one of the smallest—422.5 mg. Corrected brain weights Fixed brain weights were obtained as described in Chapter 2. The effects of the variables sex, age, body weight, litter size and parity on brain weight were determined by multiple regression as in Chapter 2. Standardizing brain weights to the average body weight, age, litter size, parity, and female sex can minimize the effects of these variables on brain weight. Mapping with standardized or corrected brain weights, increases the probability of mapping only brain weight QTLs. The BXD brain weights were standardized to that of a 21.5 gm, 79-day-old female mouse (the body weight and age average across BXD strains), using the regression coefficients for body, age, and sex shown in Table 2.10. Litter size and parity data were not available for the RI strains. The sex code for a female mouse is 1 and is 0 for a male mouse. For example, the equation to standardize brain weight would be: Corrected brain weight = fixed brain weight + 4.43*(21.5 – 20) + 10.44*(1–0) + –0.18*(79 – 40). In the equation, the coefficients for body weight, sex, and age, are italicized. Corrected brain weight averages for the 26 BXD strains can be found in Table 3.1. Similarly, AXB/BXA brain weights were standardized using their respective coefficients, to a 19.5 gm, 78.8-day-old female. Corrected brain weight averages for the 24 AXB/BXD strains can be found in Table 3.2. The ABXD5F2 brain weights were standardized to that of a 40-day-old, 19 gm, female mouse, coming from a litter size of 10, and born in a litter with a parity of three.
Table 3.1. Corrected brain weight and body weight data for BXD strains and parentals, C57BL/6J and DBA/2J.
Table 3.2. Corrected brain weight and body weight data for AXB/BXA strains and parentals, A/J and C57BL/6J.
Genotyping The BXD and AXB/BXA RI strains have already been genotyped at approximately 600 and 700 loci, respectively. (Marshall et al., 1992; Sampson et al., 1998). For the ABXD5F2 progeny, I performed a genome-wide screen by typing 126 microsatellites dispersed at an average interval length of 30 cM across the entire genome, Chr Y excepted (Fig. 3.1). Genomic DNA was isolated from spleens of the intercross progeny using the simplified DNA isolation procedure described by Laird et al. (1991), with minor modifications. Details of the genotyping procedure are available on the WWW at (http://nervenet.org/papers/PCR.html). Microsatellites were typed using the polymerase chain reaction (PCR). The PCR protocol was set up as described by Dietrich et al. (1992). A PCR reaction contained (10 µl): 1X PCR buffer, 1.92 mM MgCl2, 025 U/µl Taq polymerase (0.5 U), 0.2 mM dNTPs, 132 nM Mit map pairs and 50 ng genomic DNA. The map pairs were purchased from Research Genetics, Huntsville, AL. A loading dye (60% sucrose, 1.0 mM cresol red, 11% in-assay) was added to the reaction before the PCR. Polymerase chain reactions were carried out in 96-well microtiterplates, which allowed the use of a 12-channel multichannel pipettor to dispense reagents and load gels. I used the high stringency thermocycling protocol called "touchdown" described by Don et al. (1991). The protocol is 94° for 3 min., followed by 5 cycles of (94° for 30 sec, 60°C and then –2°C with each cycle, and 72° for 2 min). The protocol then continues with 30 cycles of 94° for 30 sec, 50° for 2 min. and 72° for 2 min., with a final cycle at 72° for 7 min.
Figure 3.1. Microsatellite marker positions for ABXD5F2 intercross screening.
The PCR products were separated by electrophoresis in 3% Metaphor agarose gels (FMC Bioproducts, Rockland ME.) in 1X TBE buffer. Gels were generally run for 90 min at 170 V, and maintained below 30 °C with cooled circulating buffer. PCR products were visualized by in-gel staining with ethidium bromide (Fig 3.2). Most loci could be scored as homozygous or heterozygous with complete confidence. To detect QTLs in the ABXD5F2 progeny, I genotyped ~4% of with the lowest corrected brain weights and ~4% with the highest corrected brain weights (the lowest 22 cases and the highest 23 cases). These 45 extreme cases were chosen because with the addition of the two parentals and F1 DNA the number of DNA samples equaled 48, which used exactly half a microtiter plate, and allowed the testing of two markers per plate. To determine the effect size of a particular QTL, all the F2 progeny were genotyped.
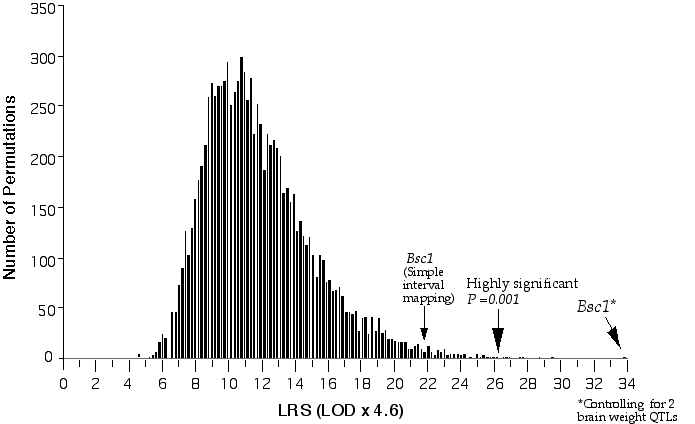
Linkage analysis for a quantitative trait involves comparing the trait means of the different marker classes, i.e., parental and recombinant genotypes AA, AB, BB. A significance difference between trait values between the different classes indicates a linkage between the genetic marker and the QTL and this can be tested by an analysis of variance (Kearsey and Pooni, 1996). I used the computer program Map Manager QT to perform linkage testing (Manly, 1996). Map manager QT reports the measure of linkage between a test interval and the phenotype with a likelihood ratio statistic (LRS). The LRS is computed by taking the n loge of the ratio of the sum of squares (SS) of the groups over the SS of the total regression. A linkage statistic is commonly reported with a LOD score (logarithm of the odds). The LOD score represents the log10 of the ratio of two probabilities, that of linkage, and that of no linkage. The LRS statistic is essentially equivalent to a LOD score and can be converted by dividing it by 4.61. The ability to detect and positionally map a QTL depends on how close the marker is to the QTL. When regions of the map are not adequately covered with markers a procedure called interval mapping can increase the ability to detect and accurately position a QTL. Interval mapping uses simple linear regression equations to predict additive phenotypic deviation at intervening positions between flanking markers. The predicted additive or dominant deviation coefficients are computed across the interval and compared to the observed additive deviation coefficients and at each position a residual sum of squares (RSS) is calculated (Haley and Knott, 1992). A QTL effect and positional assignment can be seriously skewed by the presence secondary QTLs outside the QTL interval. To eliminate this interference I performed composite interval mapping, in which QTLs mapping outside the interval were fitted as cofactors in a multiple regression analysis (Jansen, 1993; Zeng, 1994). I used Map Manager QT to perform composite interval mapping. Significance levels In testing multiple markers in a genome-wide scan one will obtain significance associations just by chance. Therefore, it is necessary to determine the probability of a significant linkage in genome-wide test. The genome-wide probability thresholds can be determined with a permutation test. A permutation test shuffles the trait data, reassigning the data to new individuals and then compares this "null distribution" with the genotypic pattern (Churchill and Doerge, 1994). The trait data is then reshuffled from 1,000 to 10,000 times and after each permutation the single best linkage statistic is recorded. The genome-wide significance thresholds are computed from the incidence of test statistics in the complete permutation test. For example, if the highest linkage statistic was reached only once in 1000 permutations, then the probability of obtaining that high a linkage statistic by chance is 1 in 1000. The statistics obtained with the experimental data are compared to the distribution of permutation scores to determine their genome-wide probability. The false positive rates of 0.63, 0.05, and 0.001 correspond to a suggestive, significant, and highly significant linkage. The advantage of using permutation tests is that the threshold values are specifically tailored to the parameters of a given data set, e.g., chromosome number, genetic length, genetic marker density, and trait distribution. I used the program Map Manager QT to perform the permutation tests (Fig. 3.3). I computed conditional empirical thresholds (CET) to control for the effects of secondary QTLs (Doerge and Churchill, 1996).
Figure 3.3. Permutation of BXD brain weight data for conditional genome-wide significance testing. The BXD data set was permuted 20,000 times at 1 cM intervals across the genome with conditional loci, R1Rik100 and Iapls2-13. The suggestive LOD, (p =0.63), is 1.2, the significant LOD, (p =0.05), is 3.1 and the highly significant LOD, (p =0.001), is 5.7.
Results
Recombinant inbreds The best match with variation in brain weight was found at D11Mit53. The correlation coefficient between brain weight and alleles, assigned either a 1 and 0 at D11Mit53, is +0.90 (Table 3.3). The underlined alleles indicate discordance with the brain weight phenotype. In Table 3.3, the allele assignments are based on the strain’s average brain weight resemblance to that of C57BL/6J (B) or DBA/2J (D). The U stands for unknown genotype and is assigned for phenotypes between that of the parentals. There are five strains that have intermediate genotypes. Refer back to Fig. 2.3A for the parental brain weight distribution. A linkage analysis with corrected BXD brain weights resulted in a LOD score of 4.7 at D11Ncvs74 at 0 cM on proximal Chr 11 and at 12 cM a LOD score of 4.5 at D11Mit53. Interval mapping on Chr 11 increases the LOD score to 5.2 between Glns-ps1 and D11Mit53. Glns-ps1 and D11Mit53 map to 8.6 cM and 12.1 cM, respectively. The concordance of brain weight variation and alleles at Glns-ps1 and D11Mit53 is shown in Table 3.3. To map secondary QTLs that may not be detected due to the interference of D11Mit53, I tested for linkage while controlling for the variance associated with D11Mit53. This resulted in detecting secondary QTLs on distal Chr 1 at D1Rik100 with an LOD of 2.8 and on mid Chr X at Iapls2-13 with LOD 2.8. Table 3.3. BXD strain distribution pattern for brain weight and genotypes at five loci on Chr 11
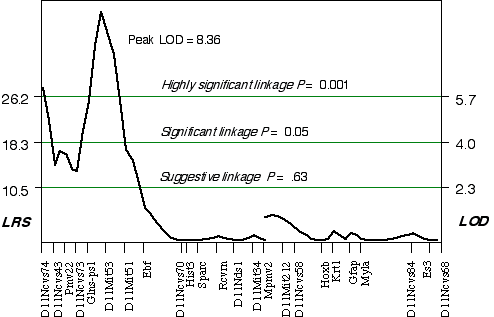
Composite interval mapping on Chr 11 with the two secondary loci as cofactors resulted in an LOD score of 5.1 at D11Ncvs74 and a peak LOD score of 8.4 between Glns-ps1 and D11Mit53, at 12 cM (Fig. 3.4). A 2 LOD confidence interval (CI) will have a 99% probability of containing the QTL. The 2 LOD CI for the QTL linked to D11Mit53 is between 11–16 cM. Correcting for the variance of the secondary loci increases the ability to detect QTLs and to accurately map and estimate QTL effects. A permutation performed on this data set defined the conditional empirical threshold for a highly significant linkage to be 5.7 (Fig. 3.3). The brain weight QTL mapped to proximal Chr 11 at 12 cM, exceeds the highly significant threshold. Thus, there is less than 0.001 probability that the linkage is spurious in a genome-wide scan! This QTL has been named brain size control 1 (Bsc1).
Figure 3.4. Linkage map demonstrates the QTL Bsc1 on Chr 11 in the BXD data set.Linkage statistics were computed at 1 cM intervals while controlling for D1Rik100 on distal Chr 1, and Iapls2-13 in middle of the X Chr.
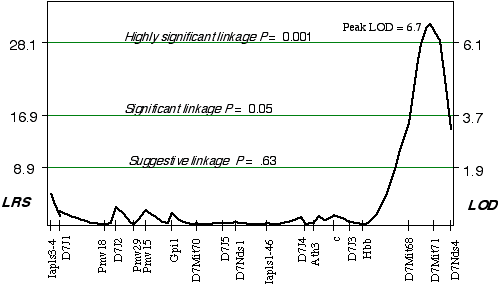
Linkage analysis in the AXB/BXA strains indicated that a gene modulating brain weight is close to a marker on distal Chr 7. Using simple linear regression, the peak LOD on distal Chr 7 at D7Mit71 was 3.8. The correlation coefficient for alleles at D7Mit71 and brain weight is +0.72. Controlling for this QTL interval on Chr 7 indicated a linkage on proximal Chr 14 (D14Mit14 and D14Mit48), with an LOD of 3.0 using interval mapping. Composite interval mapping on Chr 7, while controlling for the proximal Chr 14 region increased the LOD score on distal Chr 7 at D7Mit71, to 6.7 (Fig. 3.5). Permuting the trait data 10,000 times with the conditional locus on Chr 14, resulted in only 1 in 1000 tests as significant as the strain distribution pattern at D7Mit71. The QTL mapped to proximal Chr 7 at 65.2 cM, with a 2 LOD CI between 64-72 cM, exceeds the highly significant threshold! This QTL is named Brain size control 2, (Bsc2).
Figure 3.5. Linkage map demonstrates the QTL Bsc2 on Chr 7 in the AXB/BXA data set. Linkage statistics were computed at 1 cM intervals while controlling for loci D14Mit14 and D14Mit48.
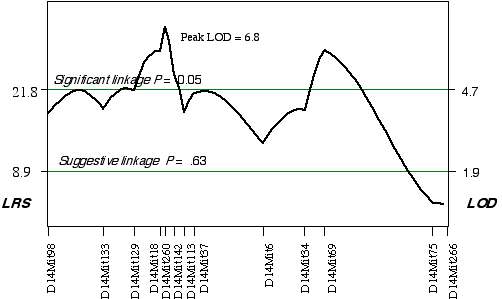
ABXD5F2 Intercross progeny An association was found between brain weight variation in the 45 extreme ABXD5F2 progeny and their genotypes at two loci on Chr 14. Linkage testing resulted in LOD scores on Chrs 14 of 5.8 at D14Mit260 and 5.4 at D14Mit69. Three secondary QTLs were identified, one on mid Chr 8 at D8Mit242 with an LOD score of 4.3, one on distal Chr 5 at D5Mit291 with an LOD score of 3.6, and one on proximal Chr 18 at D18Mit36 with a LOD score of 3.0. Controlling for the Chr 14 interval increased only the LOD score at Chr 18 at D18Mit36 to 3.7. A permutation test defined the LOD score required for a significant linkage to be 4.7. Thus, the linkage at D18Mit36 is only suggested. Composite interval mapping while controlling for D18Mit36 boosts the LOD score at D14Mit260 and D14Mit69 to 6.8 and 5.9, respectively (Fig. 3.6). The QTLs on Chr 14 map to 25 cM with a 2 LOD CI between 20–30 cM and to 59.1 cM, with a 2 LOD CI between 50–69 cM. Permuting the ABXDF2 trait data 5000 times with the conditional locus on Chr 18, resulted in only 0.7% and 1.6% of the tests with LOD scores as high as D14Mit260 and D14Mit69, respectively. Thus, these two QTLs exceed the significant threshold, p < 0.05 and have been named Brain size control 3 (Bsc3) and Brain size control 4 (Bsc4). In the AXB/BXA cross, a secondary QTL was detected on proximal Chr 14 between markers D14Mit14 and D14Mit48, loci that map to 0 cM and 13 cM, respectively. The peak linkage statistic was at 9 cM. The Chr 14 committee report places D14Mit48 a little more distal at 16.5 cM. The Chr 14 QTLs in the ABXD5F2 cross, D14Mit260 and D14Mit69, map to 25 cM and 59.1 cM, respectively. These are close to the positions reported by the Chr 14 committee, 29 cM and 43 cM, respectively. The secondary QTL identified in AXB/BXA strains is too proximal to be the Bsc2 in ABXD5F2. However, the secondary QTL in AXB/BXA does give credence to the small increase in the linkage statistic proximal to the D14Mit260, between markers D14Mit98 and D14Mit144 (Fig. 3.6).
Figure 3.6. Linkage map demonstrates the QTLs Bsc3 and Bsc4 on Chr 14 in the ABXD5F2 data set. Linkage statistics were computed at 1 cM intervals while controlling for the locus D18Mit17.
QTL effect size To examine the effect size of QTLs on Chr 14 and Chr 18 in the ABXD5F2 cross I performed a regression analysis on the brain weight z-scores for each genotype class. A single allelic substitution at the QTL linked to D14Mit260 is responsible for an effect size of 0.3 SD units, with a 95% confidence interval equal to ± 0.21. An analysis of variance determined that the regression was highly significant ( p < 0.0001) and that variance at D14Mit260 accounts for 5.9% of the variance in brain weight. The standard deviation of the corrected brain weights for ABXD5F2 is 21.7. Thus, each allelic substitution at Bsc3 translates into ~6.5 mg difference in brain weight. The effect of a single allelic substitution at the QTL near D14Mit69 is also equal to 0.3 SD ± 0.23, explains 5.1% of the variance, and each allelic substitution translates into ~ 6.5 mg difference in brain weight. The effect of a single allelic substitution at the QTL near D18Mit20 is equal to 0.25 SD ± 0.23, explains 3.5% of the variance, and produces a ~5.4 mg difference in brain weight. The heritability estimate for ABXD5F2, reported in Chapter 2, is 24%. Adding the explained variance of the three QTLs equals 14.5%, therefore, together they explain 60% of the genetic variance and 15% of the total phenotypic variance in brain weight among ABXD5F2 progeny.
Discussion I have mapped four QTLs that have major effects on brain weight in mouse to Chrs 7, 11, 14. These brain weight QTL have been named Bsc1, 2, 3, and 4. Bsc1 maps proximally to Chr 11 at 12 cM, Bsc2 maps distally to Chr 7 at 65.2, and Bsc3 and Bsc4 map to Chr 14 at 25 cM and 59.1 cM, respectively. Secondary brain weight QTLs were mapped to Chrs 1, 5, 8, 11, 14, 18, and X. In Chapter 2, a correlation between albino coat color and brain weight in the AXB/BXA strains indicated that a QTL controlling brain weight mapped near the albino allele on distal Chr 7. The significant linkage between brain weight and D7Mit71 on distal Chr 7 in the AXB/BXA cross confirms the linkage between coat color and brain weight. A secondary QTL was mapped to the X Chr in the BXD set. I looked for evidence of a sex-difference in brain weight among reciprocal C57BL/6J and DBA/2J F1 males, since they inherit their X Chr from different strains. There was no difference in brain weight between reciprocal hybrid males. However, this comparison was not paired; there were 6 B6D2F1 males and 18 D2B6F1 males. Regardless the similarity of reciprocal F1 males does not preclude a sex association because detection could be confounded by autosomal variation if the effect size is too small. A study by Belknap et al. (1992) mapped suggestive QTLs controlling brain weight in BXD strains to Chrs 2, 6, 7, 11, and 13. The locus Belknap identified on Chr 7 was proximal around 14 cM, while my AXB/BXA analysis detected a QTL on distal Chr 7. The loci identified on Chr 11 by Belknap are proximal, including Pmv-22, Glns, and Hba, which map between 8 cM and 16 cM. In my BXD mapping analysis, the best linkage to brain weight variance was between 11 cM and 16 cM, at Glns-ps1 and D11Mit53, respectively, with the peak LOD score at 12 cM. Therefore, I have confirmed the Chr 11 QTL reported by Belknap et al. (1992). There are several explanations why I did not confirm more of the QTLs detected in the Belknap et al. (1992) study. First, the Belknap study used only 20 strains, whereas I use 26. Second, in the Belknap study the brain weights were regressed with respect to body weights by computing brain to body weight ratios, rather than a regression analysis. And third, the significance of Belknap's QTLs are only suggestive since they are nominal p values, whereas mine are genome-wide significant. Effect size Hundreds of genes are probably involved in controlling neuron number, however, only a dozen or so contribute to the variation in cell number. Many of these QTLs will have small effects on global neuron number while some will are large effects. It is the genes with large effects that will be detected in a linkage analysis, and thus, the four brain weight QTLs are expected to have relatively large effect size. The two QTLs mapped on Chr 14 in the ABXD5F2 cross, account for 5.9% and 5.1% of the phenotypic variance in brain weight. In addition, the suggestive QTL mapped in the ABXD5F2 cross on Chr 18, accounts for 3.5% of the phenotypic variance in brain weight. The explained variance estimates are not likely to be overestimates since the sample size of the ABXD5F2 cross (n =522) is large enough for reliable estimates of effect size. Thus, in the ABXDF2 cross, three major effect QTLs account for 60% of the genetic variance and contribute to ~15% of the phenotypic variance in brain weight. Surprisingly, significant QTLs were not identified in multiple crosses. Thus, each cross has unique major effect brain weight QTLs segregating, despite some common origins of the parental strains. In addition to the two major brain weight QTLs mapped to Chr 14 in the ABXD5F2 cross, a secondary QTL on proximal Chr 14 was mapped in the AXB/BXA strains. The detection of three QTLs for brain weight on Chr 14 indicates that brain weight QTLs cluster on Chr 14. Candidate Genes The complexity of a quantitative trait can limit the precision to which a QTL can be mapped, making the direct cloning of the QTL intractable. However, due to the large number of genes that are already cloned, in many cases, positional cloning will not be necessary. One can simply search for candidate genes that map within the QTL interval. Candidates would have a compatible function or expression pattern, or, when mutated, disturb the phenotype under study. For instance, the tubby gene was a candidate for a QTL controlling diet-induced obesity susceptibility in mice because a mutation in tubby, which mapped to the same region as the QTL, caused a severe mouse obesity phenotype (Kleyn et al., 1996). Most QTLs have been identified fortuitously in this way, whereby a gene is recognized by a major morphological mutation and genetic variants among strains are subsequently found. A search for brain weight QTL candidates was performed using the Portable Dictionary of the Mouse Genome developed by Robert Williams and attainable through the web (http://mickey.utmem.edu/front.html) (Williams, 1994), and from the Mouse Genome Informatics (MGI) database, located at the Jackson Laboratory (http://www.informatics.jax.org/). The human genome was also inspected for candidate genes in mouse conserved-synteny regions using a homology search in the MGI database. QTL candidates were selected if they mapped within the QTL interval, are expressed in the brain, and are known to be involved in cell proliferation, or when absent or mutated disrupt brain development. Two candidates for the secondary QTL that mapped to the proximal end of Chr 11, between 0 and 1 cM, are the mouse homolog of the human gene neurofibromatosis type 2 (NF2) and the beta subunit of brain-specific Ca2+/calmodulin-dependent protein kinase II (Camk2b). The human NF2 gene encodes a tumor suppressor protein called schwannomin. A mutation in NF2 causes an autosomal dominant disorder that increases the chance of developing benign tumors in the nervous system. The expression of NF2 is found on embryonic days 15 and 16 in cells that are migrating from the ventricular zone to the cortical plate. NF2 is likely to play a role in controlling cell proliferation, perhaps in onset of differentiation. The candidate Camk2b is first expressed in the brain on E12.5 and continues to be expressed in adult brain. The specific role that Camk2b performs in the brain is unknown. A number of potential Bsc1 candidates map within the 2 LOD CI between 11 cM and 16 cM on Chr 11. These include RAB1, a member of the RAS oncogene family, Krct, a member of a novel subfamily of serine/threonine kinases, Otx1, creatine kinase brain, related sequence 5 (Ckb-rs5), epidermal growth factor receptor (Egfr), and epidermal growth factor receptor-related sequence, (Egfr-rs). All of these genes are expressed in the brain. Otx1 is an attractive candidate because of its role in cortical neurogenesis. Otx1 is expression in mouse begins at E10 in the rostal brain and continues until late gestation. Mice homozygous null for Otx1 have defective sense-organ development and neurogenesis (Suda et al., 1999). Egfr maps to 9.0 cM, a little too proximally for Bsc2, but was thought to be an attractive candidate because of EGF’s effect on cell proliferation (see Introduction–developmental control of neuron number). However, EGFR has been dismissed as a candidate because the average brain weights from mice carrying a mutation in EGFR called waved-2 (wv2) are the same as wildtype brains (wv2– 488 ± 20.7, n =4 and wt– 485 ± 9.0, n =12). The mutant wv2 has a single point mutation in EGFR that produces a 5–10 fold decrease in autophosphorylation and over a 90% reduction in substrate phosphorylation (Leutteke et al., 1994). The best Bsc2 candidate is Msx3. The gene Msx3 maps to 69 cM on Chr 7 within the 2 LOD CI for Bsc2 and is expressed in the ventricular zone of the dorsal neural tube during early development (Wang et al., 1996). The best Bsc3 candidate is orthodenticle, Otx2. Otx2 maps to 20.5 cM on Chr 14, is expressed in the developing central nervous system, and plays an important role in regional morphogenesis of the anterior brain structures (Suda et al., 1999). Unfortunately, I did not find any candidate genes for Bsc4 on distal Chr 14. This brain weight mapping study has identified the location of four brain weight QTLs. In addition a survey of candidate has suggested some exciting candidates for brain weight QTLs. In particular three homeobox containing genes, Msx, Otx1 and Otx2. Homeobox genes have been suggested to function in some instances, as a regional proliferation index. Furture studies could involve testing some of these candidate genes. However, narrowing the QTL interval will probably be necessary to determine the best candidate and proceed with cloning. It will be exciting to discover the identity of the genetic variants and the mechanism by which they influence brain weight. In addition, the influence of these genetic variants in the variation of brain weight in other species can be tested to determine if there are common evolutionary mechanisms, as expected. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Neurogenetics at University of Tennessee Health Science Center
| Text Only | Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org