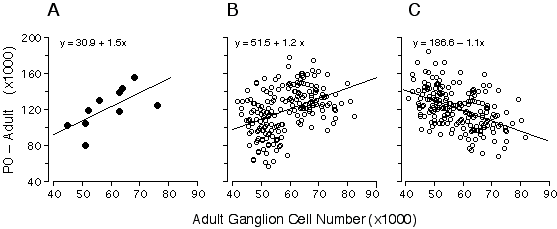 |
| ||||||
 | |||||||
| ||||||||
|
| ||||||||
|
Home  Publications |
|
|
Genetic Analysis of Variation in Neuron Number Richelle Cutler Strom Chapter 6: Developmental Mechanisms Controlling Retinal Ganglion Cell Variation Among Inbred Mouse Strains Introduction The distribution of ganglion cell strain averages for 57 inbred mouse strains is bimodal, with distinct modes centered at 55,000 and 64,000. Most of the bimodality in strain averages is controlled by a major effect QTL, neuron number control 1 (Nnc1). This QTL is located on Chr 11 and is closely linked to three genes known to influence retinal development—the retinoic acid receptor alpha, neuregulin, and the thyroid hormone receptor. Nnc1 could influence ganglion cell number by modulating either cell production or the severity of natural cell death. My principal objectives in this study were to determine the developmental mechanism by which allelic variants at Nnc1 control neuron number, and to assess the relative contributions of cell production and cell death in the consistent and pronounced differences in ganglion cell among strains of mice. I examined ganglion cell production in ten strains—four selected from the low mode, four from the high mode, and one each from the high and low extreme (Fig. 1). I included the strains C57BL/6J and DBA/2J—the parental strains of the BXD RI set in which Nnc1 was mapped. Mechanisms generating neuron number differences between these two strains can be confidently assigned to Nnc1. Total ganglion cell production was estimated by counting retinal ganglion cell axons at birth, a time at which ganglion cell generation in mice is complete (Dräger, 1985), but before significant ganglion cell death has begun (Linden and Pinto, 1985). The results of this study have been published (Strom and Williams, 1998).
Materials and methods Mice As illustrated in fig. 6.1, strains of mice were chosen primarily to represent the two major modes in ganglion cell number. Three standard inbred strains were selected from the low mode (C57BL/6J, A/J, and LP/J) and four standard inbred strains were selected from the high mode (BALB/cJ, C3H/HeSnJ, CE/J, and DBA/2J). All of these strains were obtained from the Jackson Laboratory, (Bar Harbor, ME). In addition, I selected two strains—CAST/Ei and BXD32—that have exceptionally low and high ganglion cell numbers, respectively. BXD32 was obtained from Dr. Benjamin Taylor at the Jackson Laboratory. CAST/Ei is an inbred strain derived from M. musculus castaneus that I obtained from Dr. Eva Eicher at the Jackson Laboratory. Finally, I studied an outbred sample of Mus caroli that I refer to as CARL/ChGo, a strain that falls into the low ganglion cell mode. CARL/ChGo is a partially inbred strain of M. caroli given to us by Dr. Dan Goldowitz at the University of Tennessee. Both CARL/ChGo and CAST/Ei are representatives of wild species endemic to Southeast Asia. All mice were mated at the University of Tennessee mouse colony to produce neonates. The day of birth was designated postnatal day zero (P0).
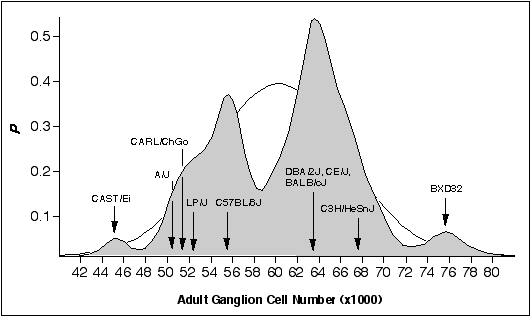Figure 6.1. Bimodal distribution
of adult ganglion cell averages for 60 inbred strains. The strains
include 38 recombinant inbred strains and 17 standard inbred strains listed
in Chapter 4, and 5 additional strains. A Gaussian probability distribution
was computed for each strain and summed to obtain a probability density plot
(see Chapter 2, (Williams et al., 1996). The figure shows that most strains
fall into two main modes. The Gaussian function drawn in the background has
a mean of 60.6 ± 6.3 (x1000), the average and SD of the 60 strains. The
arrows designate the strain averages for the ten strains examined in this
study.
Tissue fixation The neonates were anesthetized by placing them on ice for several minutes. Neonates were then perfused transcardially with 0.1 M phosphate buffered saline (0.9%), followed by fixative (2.5% glutaraldehyde and 2.0% paraformaldehyde in 0.1 M phosphate buffer). Midorbital segments of optic nerves were dissected from the neonates, osmicated, and embedded in Spurr’s resin. Nerves were thin-sectioned, placed on formvar-coated grids, and stained with lead citrate and uranyl acetate. Estimating ganglion cell number I estimated ganglion cell numbers by counting axons in P0 optic nerve cross-sections. Axons were counted as described in Chapter 4, Methods section, with the following exceptions. Nerves were photographed in a grid pattern at ~X30,000 using a JEOL EX2000II electron microscope. Unmyelinated axons were easily identified and counted (Fig. 6.2)
I counted necrotic axons in neonatal optic nerves from two strains belonging to the high mode and two strains belonging to the low mode. I did this by systematically scanning the entire optic nerve cross-section for necrotic axons at X15,000. The criteria for distinguishing necrotic axons are those described in Williams et al., (1986). I also searched for growth cones in the sample of photographs used for counting axons and by scanning several optic nerves at high magnification (>X40,000).
Results The retinal ganglion cell population at birth ranged from 131,000 to 224,000 (Table 6.1). The mean for all 46 cases is 182,500 ± 4,400 SE. This value is almost three times higher than the average for an equally diverse sample of adult mice (see Chapter 4, (Williams et al., 1996)). I counted an average of five neonates per strain. The coefficient of variation within strains averaged 8.2%—only slightly higher than the 7.2% value obtained for adult mice (see Chapter 4, (Williams et al., 1996)). The small increase is probably due to the technical difficulty of counting axons before they are myelinated. Given the anticipated variation in the stage of maturation of sets of neonatal mice sacrificed at birth, this CV is low and suggests that the ganglion cell population within a strain is comparatively stable at this stage of development. The average coefficient of error (the standard error divided by the sample mean) averaged 4.5% in neonates and 2.5% in adults. These values provide an assessment of the reliability of adult and neonatal ganglion cell counts.
Table 6.1.Ganglion cell number and percentage cell loss
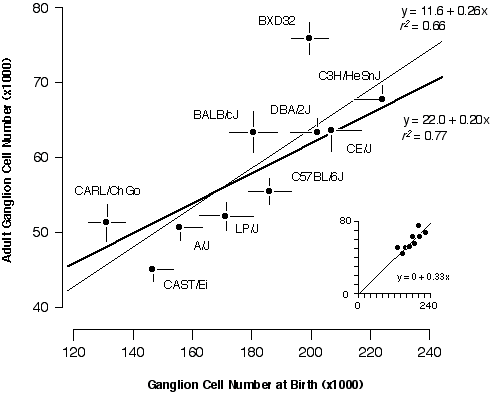
Cell Production If strain differences in adult ganglion cell numbers result from differences in the number of neurons that are generated, then at birth each strain should have a population that is approximately three-fold higher than its adult mean. The slope of the regression should be close to 1:3 and the correlation should be high. This is almost exactly what I found. The slope of a free regression for the ten strains is 0.26 ± 0.07 (Fig. 6.3). Forcing the regression line through the origin produces the expected slope of 1:3 with an excellent fit (inset to Fig. 6.3). The positive y-intercept (11,600 adult cells) in the free regression may result from sampling error, non-linearity of cell death, or may indicate a basal level of cell production. The correlation coefficient of the free regression in Fig. 6.3 is 0.81, and the corresponding coefficient of determination (r2) is 0.66. Thus, two-thirds of the variance in adult cell number can be readily explained by strain differences in cell genesis.
I was particularly interested in understanding the process that produces bimodality in adult strain averages and for this reason I also restricted the analysis to the eight strains belonging to high and low modes (Fig. 6.3, bold line). The coefficient of determination for this subset of points is 0.77, indicating that the bimodality is generated primarily by differences in ganglion cell production. The remaining "unexplained" variance must result from strain differences in the severity of cell death, developmental noise, and technical error. This statistical analysis is complicated by two factors. First, the parameters plotted in Fig. 6.3 are dependent—total cell production cannot be less than the adult population. Second, the distribution of adult values is far from normal (Fig. 6.1). Conventional statistical estimates are therefore difficult to interpret. To address these problems I carried out Monte Carlo simulations to test cell production and cell death models using seed parameters taken from the adult distribution (Fig. 6.4). I subtracted the adult population from the neonatal population to insure independence between the parameters (Fig. 6.4A). Figures 6.4B and 6.4C show the outcomes of two typical Monte Carlo simulations in which I plotted adult cell number against the number of lost cells. The first model (Fig. 6.4B) assumes that all differences in adult cell number are caused by matched differences in cell production and that cell death is strictly proportional to cell production. The second model (Fig. 6.4C) assumes that all differences among adult strains are caused by variation in the severity of cell death and that at birth all strains have roughly the same cell population (~180,400 ± 18,400 cells). In the cell production simulation (Fig. 6.4B), the regression slope is +1.2, whereas in the cell death simulation (4C) the slope is –1.1. My actual data set (Fig. 6.4A) with its slope of +1.5 strongly supports a cell production model.
Figure 6.4. Regression of numbers of cells that are lost (number at P0 minus the number at maturity) and adult ganglion cell number from our data.(4A), and two alternative Monte Carlo simulations (B and C). The first model (B) assumes that all differences in ganglion cell number are caused by cell production differences, whereas the second model (C) assumes that all differences are caused by variation in the severity cell death. Monte Carlo data sets consisted of 200 numbers randomly selected from normal distributions. In both models, high and low adult ganglion cell groups, (n = 100 each), were selected from two normal distributions with seed parameters (mean and standard deviation) from the 5 high (66,800± 5,400) and 5 low (50,920 ± 3,800) strains that I studied. In the production model (B), means were obtained from two normal distributions with seed parameters (mean and standard deviation) from the 5 high (202,680 ± 15,500) and 5 low (158,100 ± 21,200) strains. In the case of the cell death model (C), where no production differences are assumed, the neonatal means were obtained from a single distribution, with a mean and standard deviation of all 10 strains combined (180,390 ± 18,400). The slope obtained with our real data is +1.5 (A), while the cell production (B) and cell death (C) models are +1.2 and –1.1, respectively. The positive slope from our data is close to that of the simulated cell production model, demonstrating that differences in adult ganglion cell number is predominantly due to differences in cell production. In used Model I linear least-square regression for this analysis because the measurement error term is without bias. Adult ganglion cell number was subtracted from P0 ganglion cell number to make the y-axis formally independent of adult ganglion cell number plotted on the x-axis.
The 10 inbred strains were divided into high (BALB/cJ, C3H/HeSnJ, CE/J, BXD32, and DBA/2J) and low groups (C57BL/6J, A/J, CAST/Ei, CARL/ChGo, and LP/J). Mean adult ganglion cell numbers for these groups are 66,800 ± 2,700 and 50,900 ± 1,900, respectively. There are highly significant differences in ganglion cell production between these groups, with means of 202,700 ± 7,800 and 158,100 ± 10,600, respectively (t test, p < 0.001). In contrast, there is no significant difference in the percentage of ganglion cell loss between high and low groups, with mean percentage cell loss relative to neonatal values of 66.9% and 67.5%, respectively (p = 0.42). Nnc1 was mapped using recombinant inbred strains generated from the parental strains, DBA/2J and C57BL/6J. For this reason a comparison between these two strains is especially germane in discovering how Nnc1 modulates ganglion cell number. The severity of percentage cell death was closely matched between DBA/2J and C57BL/6J—69% and 70%, respectively. In contrast, DBA/2J produces ~16,400 more cells than C57BL/6J. This result, together with our previous finding of additive gene action (see Chapter 5, and , indicates that the substitution of a single allele at Nnc1 is associated with a production difference of approximately 8,000 cells. Cell Death With the exception of strains BXD32, CARL/ChGo, and BALB/cJ, the average percentage of cell death among strains is relatively uniform—69% ± 1.2% (Table 6.1). While the percentage of cell death is relatively uniform, the absolute magnitude of ganglion cell death is variable among strains and is highly correlated with production values (Table 6.1). There are some notable exceptions to this generality. The percent cell death in BXD32 and CARL/ChGo is significantly lower than in other strains (t test, p < 0.05, with Bonferonni correction). Estimates of ganglion cell production are similar in BALB/cJ and C57BL/6J, yet these strains have adult populations that differ by about 8,000 cells (Table 6.1). A slight reduction in the severity of cell death in BALB/cJ (65% loss) appears to account for this strain’s relatively high cell number at maturity. In this instance, the marked strain difference in adult population size results primarily from variation in the severity of cell death. Differences in cell death can also compensate for differences in cell production. For example, CARL/ChGo produces an average of 131,000 ganglion cells—20,000 to 40,000 fewer cells than A/J and LP/J, respectively—yet all three strains have very closely matched adult populations (Table 6.1.). Necrotic axons and growth cones The validity of our quantitative analysis depends on the assurance with which I can estimate total ganglion cell production in mice. If much cell loss occurs before birth or much cell addition occurs after birth, then production estimates based on axon counts in the optic nerve at P0 will be too low. To rule out the possibility that significant cell death occurs prenatally, I counted necrotic axons in neonatal optic nerves from strains belonging to the high and low modes using criteria described by Williams and colleagues (1986). Necrotic axons are relatively easy to see, and it was practical to count all sites of necrosis in a single optic nerve cross-section. Necrotic axons at P0 make up 0.02% and 0.05% of the fiber population in cases selected from the low strains, A/J and C57BL/6J, respectively, whereas they make up 0.07% and 0.09% of the population in cases selected from the high strains, BXD32 and C3H/HeSnJ, respectively. The fact that a somewhat higher incidence of necrosis was noted in nerves taken from the high strains makes it very unlikely that variation in early axon loss accounts for differences between adult values. Growth cones were exceeding rare in all material and fewer than 5 profiles among all cases met even a relatively lax criteria for these structures (Colello and Guillery, 1992; Williams et al., 1986). Specificity of strain differences Do strain differences in retinal ganglion cell number correspond to differences in total brain weight or are differences among strains specific to the ganglion cell population? The correlation of ganglion cell number and brain weight across individual mice is 0.37, but when strain averages are used the correlation rises to 0.75. This suggests that about half the variance in neonatal ganglion cell number can be explained directly or indirectly by differences in brain weight. As assessed by quantitative DNA analysis, brain weight differences among neonatal mice are primarily due to differences in total cell number (Zamenhof and van Marthens, 1978). Thus, mechanisms modulating ganglion cell number may have common effects on cell number in the other parts of the CNS. Alternatively, the correlation between ganglion cell number and brain weight could suggest that variation of ganglion cell number is the result of differences occurring very early in a neural progenitor pool, perhaps during neurulation. The correlation between strain averages of adult brain weight and ganglion cell number for the same strains is only 0.51. Given the wide confidence intervals of correlations computed with low numbers of cases, the difference between the adult and neonatal correlations (0.51 and 0.75, respectively) may be due to sampling error. However, it is also conceivable that strain variation in cell death decreases an initially high correlation between brain weight and retinal ganglion cell number. In any case, the cellular specificity of the strain differences is likely to be low, and I expect differences in numerous other neuronal cell populations to be closely matched with the differences I find in ganglion cell number. Discussion The analysis demonstrates that most of the variation in adult ganglion cell number among strains of mice can be traced to differences in cell production. Allelic variants at the Nnc1 locus on Chr 11 generate the pronounced bimodality in ganglion cell population size by modulating ganglion cell production. Generation and death of retinal ganglion cells Generation of retinal ganglion cells in mice begins on E11 and lasts until just before birth (Dräger, 1985). There is a short delay between neurogenesis and the time at which ganglion cell axons extend into the optic nerve (Colello and Guillery, 1992). This delay could deflate estimates of total cell production. However, very few ganglion cells are produced after E18 and as anticipated from the work of Colello and Guillery (1992), I did not find growth cones in neonatal optic nerves. It is therefore unlikely that the estimates of total production are biased downward by late ganglion cell generation. In contrast, ganglion cell death begins at, or just before, birth, peaks between postnatal days 4–6, and is essentially complete by P12 (Linden and Pinto, 1985). At the peak of cell loss, between 5,000 and 10,000 ganglion cells are eliminated per (Williams et al., 1990). However, fewer than 2,000 cells are lost on the day of birth in mice, consistent with my observation of very few necrotic axons—less than 300 per nerve. At this rate it is improbable that more than a total of 10,000 ganglion cells are lost prenatally. In chickens there is as much as a three day delay between the onset of ganglion cell degeneration in the retina and the elimination of axons in the optic nerve (Rager et al., 1978). If there is a similar delay in mice then axon counts should preserve our production estimates. Nonetheless, the estimates of total production maybe biased downward slightly by the early loss of ganglion cell axons. However, the magnitude of this error is sufficiently small (~10,000 cells) that I did not think this loss warranted correction. Variation in retinal ganglion cell death The severity of cell death is close to 68–70% in most strains of mice. However, there are three exceptional strains with less severe loss. Three to nine percent fewer cells are lost in BXD32, CARL/ChGo, and BALB/cJ. BXD32 is particularly interesting because it has the highest adult population (75,800 ± 1,900) among the 60 strains I have now examined. Yet at birth BXD32 has an unexceptional number—199,500—that is lower than three other strains. Clearly, one or more genes controlling rates of ganglion cell death are responsible for the high adult cell number in this strain. It would be feasible to map a cell death gene by crossing BXD32 to a strain with similar ganglion cell production but higher cell death. Variation in the severity of cell death may result from differences in titers of neurotrophic factors. The neurotrophins—BDNF and neurotrophin-3/4—have been found to increase survival of retinal ganglion cells in chicken and rat (Ma et al., 1998; Rosa et al., 1993). Neuregulin, found on the cell surface and as a secreted protein, can also increase survival of neonatal rat retinal ganglion cells in culture (Bermingham-McDonogh et al., 1996). Differences in the concentration or expression time of these neurotrophic factors, their receptors, or components within their signaling pathways could produce variation in the severity of naturally occurring ganglion cell death. Nnc1 controls cell production Approximately 77% of the variation among adult strains result from differences in the production of ganglion cells. The percentage of cell death in high and low groups does not differ significantly (66.9% and 67.5%, respectively). I conclude that variation in adult ganglion cell number among inbred mouse strains results predominantly from differences in cell production. Comparison of our data with the Monte Carlo simulations (Fig. 6.4) corroborates this conclusion. A major motivation for undertaking the present study was to determine how and when allelic variants at Nnc1 influence the size of the ganglion cell population. Collectively, the results strongly indicate that Nnc1 modulates ganglion cell number by influencing cell production, and because ganglion cell production occurs before birth, this result provides a time frame for the action of Nnc1.
|
Neurogenetics at University of Tennessee Health Science Center
| Text Only | Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org