|
| ||||||
|
| ||||||||
|
| ||||||||
Home  Publications Publications |
|
|
Genetic Analysis of Variation in Neuron Number Richelle Cutler Strom Chapter 2: Genetic and Environmental Control of Brain Weight Variation
Introduction Variation in brain weight among different mouse strains could result from genetic variation in genes that are expressed only within the brain. Variation in brain weight can also result from environmental factors, such as nutritional differences resulting from variable litter size and from genetic factors, such as the expression of hormones relating to the sex of the animal or from body weight genes with pleiotropic effects. In order to estimate the proportion of variance in brain weight that results from assessable factors, I have performed linear regression analyses with brain weight and the cofactors, sex, age, body weight, litter size and parity. In fitting a regression equation, the approximate change in brain weight for a unit change in a cofactor can be estimated. To minimize the variance in brain weight attributed by these factors, brain weights were standardized to the mean age, body weight, litter size and parity. Although a number of studies have examined the effects of variation in these variables on brain weight, this study is the first comprehensive analysis of the effects of multiple factors and a comparison of these variables between strains. In this study I have also tested the feasibility of mapping genes that control variation in brain weight among mice. Before launching a mapping study, it is necessary to establish that there is an appreciable amount of heritability for the trait of interest. Studies have reported brain weight to be highly heritable, ranging from 0.70 in mice (Atchley et al., 1984; Roderick et al., 1973), to 0.75 in a primate colony of rhesus macaques (Cheverud et al., 1990). However, those estimates are only relevant to the particular population and the environment from which they were measured. Thus, as a prelude to mapping, I have estimated the heritability of brain weight among inbred strains and within mapping crosses. The accuracy of the heritability estimate depends on the precise estimate of the environmental variance within an isogenic group. For example, if the environmental variance is exceedingly high as a result of age-related variance then the genetic component could be underestimated. To compute precise heritability estimates and to estimate the number of genes producing variation in brain weight, I used corrected brain weights in which the variance due to known cofactors has been minimized.
Materials and methods Mice Most of the inbred mice were obtained from the Jackson Laboratory (Bar Harbor, ME). Environmental variation was minimized by housing the mice in a pathogen-free environment, maintained at 20-24ºC on a 14:10 hr light/dark cycle, with all mice being fed a consistent diet of 5% Agway Prolab 3000 rat and mouse chow. Standard inbred strains. The standard inbred strains were derived from domesticated hybrids generated from crosses between M. m. domesticus, M. m. musculus, and M. m. castaneus early in the 20th century (Bonhomme, 1992). The hybrids strains were produced by inbreeding through at least 20 generations of brother x sister matings and most have now been maintained by successive sibling matings for greater than 80 generations. Brain weights were obtained for 27 standard inbred mouse strains (Table 2.1). Figure 2.1. shows the lineage chart of the genus Mus with fixed brain weights for strains, species, and subspecies of mice. Inbred strains are shown in the yellow panel.Subspecies of M. musculus. Brain weights were obtained from four wild subspecies of M. musculus: (1) M. m. castaneus (CAST/Ei and CASA/Rk), a Southeast Asian subspecies; (2) M. m. musculus (CZECHII/Ei), a commensal Eastern European mouse; (3) M. m. molossinus (MOLD/Rk, M, MOLF/Ei, MOLC/Rk), a Japanese hybrid of M. m. musculus and M. m. castaneus; (4) M. m. domesticus (WSB/Ei), a commensal and widely dispersed subspecies of Western Europe and the Americas. The phylogeny and native territory of these species are reviewed in Bonhomme (1992). Species of Mus. Brain weights were obtained from inbred representatives of four wild species of Mus, Fig. 1, bottom panel: (1) M. musculus, the common house mouse, a wide-ranging and highly adaptable commensal species from which the standard strains are derived; (2) M. spretus (SPRET/Ei), a short-tailed field mouse distributed around the Western Mediterranean; (3) M. spicilegus (PANCEVO/Ei), a colonial mound-building species from Eastern Europe, (4) M. caroli (CARL/ChGo), a small tropical East Asian species. The mouse CARL/ChGo is outbred and has been maintained since the mid 1970’s in a colony of 5 to 10 breeding pairs with specific avoidance of sibling matings. Table 2.2 lists the mean brain weight, body weight, age and numbers sampled for each subspecies and species of Mus. The lineage of the subspecies and species of Mus is shown in the bottom panel of Fig. 2.1. Isogenic F1 hybrids I obtained brain weights from eleven isogenic F1 hybrids, (ABXD5F1, AC3HF1, C3HAF1, B6D2F1, D2B6F1, BXD32x5F1, PLSJF1, 32CASTF1, CCASF1, CAF1/J, CB6F1). The hybrid CAF1/J, was obtained from the Jackson Laboratory. All others were generated in the University of Tennessee mouse colony. Data for the F1 hybrids can be found in Table 2.4. Recombinant mice. In this study, I used two types of recombinant progeny, recombinant inbred strains and F2 intercross progeny. Recombinant inbred strains (RI) are made by first mating mice from two inbred strains and then crossing the F1 hybrids to produce F2 progeny. F2 mating pairs are then chosen at random and their descendants are inbred through 20 or more generations of brother and sister mating. Each F2 mating leads to an isogenic strain, homologous at all genetic loci, but with a unique mosaic of chromosomal segments derived from the two progenitors. Brain weights were obtained from 26 BXD strains and 24 AXB/BXA strains. The sex ratio is approximately equal across all BXD and AXB/BXA cases, although within some strains the sex ratio is not well balanced. The average age and the number of mice sampled within each BXD and BXA/AXB strain are shown in Tables 3.1 and 3.2.Brain weights were obtained from four F2 intercrosses: ABXD5F2 (n = 517), AC3HF2/C3HAF2 (n = 360), CCASF2 (n = 112), 32CASTF2 (n = 141). The brain weights for these mice are not shown. The AC3HF2 and C3HAF2 progeny were produced from reciprocal F1 hybrids produced by interchanging the sexes. The sex ratios within these crosses are close to 50:50. Fixation and processing of tissue Adult mice were anesthetized with Avertin (1.3% 2,2,2-tribromoethanol and 0.8% tert-pentyl alcohol in water, 0.5–1.0 ml ip). Mice were transcardially perfused with 0.9% sodium phosphate buffered saline (pH 7.4, room temperature), followed with 1.25% glutaraldehyde and 1.0% paraformaldehyde in 0.1 M PB (pH 7.3). Fixed brains were dissected at low magnification using a dissecting microscope. The brains were transected at the caudal margin of the cerebellum. Brains were weighed immediately after dissection to the nearest 0.1 mg. Paraflocculi or any other brain tissue torn away during dissection was added to the weigh pan. Small corrections were made when tissue was lost, usually a paraflocculus at ~2.5 mg. Quantitative trait genetics The two major components of phenotypic variance (VP) are genetic variance (VG) and environmental variance (VE). Examples of environmental factors are nutrition, uterine spacing, litter size, obstetrical complications, parity or age of mother and prenatal exposures (temperature, pathogens) (Jacobson, 1991). Environmental variance can also result from stochastic internal variation during development, known as developmental noise. Factors contributing to total genetic variance (VG) can be partitioned into additive gene effects (VA), dominance deviation (VD), and gene interaction (VI) (Falconer, 1989). Additive genetic variation results from allelic substitutions at genes and is estimated by the degree of resemblance among relatives. Dominance deviation occurs when one allele produces a larger effect with respect to the other. Interaction variance, or epistasis, results when different genetic loci interact and produce complex non-linear effects. Another factor contributing to phenotypic variance is the technical variance (VI ), which results from measurement error. Taking all these factors into account, phenotypic variance consists of, VP = VA + VD + VI + VE + VT. Regression analysis To estimate the effects of environmental factors on brain weight I used DataDesk 6 (Data Description, Ithaca, NY) to perform least-squares regression with the variables, sex, age, body weight, litter size, and parity. Body weight, sex and age were recorded at the time of perfusion. In the ABXD5F2 progeny, parity and litter size were also recorded. Animal records, including parentage information, cage identification, litter size, birth dates were stored in a record keeping program called Mendel’s Lab 4. Heritability In this study, I estimated the variance attributable to genetic factors by subtracting the environmental variance found among isogenic animals from the variance found among a genetically heterogenous population, (VP – VE) (Crusio, 1992). Because inbred strains tend to show greater variability due to the fixation of deleterious alleles, the environmental variance (VE) is best calculated from the weighted average of the variance within the parentals and the F1 hybrid (VE = 1/4VP1 + 1/4VP2 + 1/2VF1) (Wright, 1968). Heritability in the broad-sense measures the proportion of the total phenotypic variation in a population attributable to all genetic factors, including dominance deviation and genetic interaction. Heritability in the narrow sense measures the proportion of phenotypic variance due to additive gene effects, (VA/VP). A good approximation of narrow-sense heritability can be estimated by comparing the nongenetic variance found within inbred strains to the variance found between strains (Hegmann and Possidente, 1981). h2 = 1/2 VA/[(1/2 VA)+ VE] The estimate of VA can approximate additive genetic variance because no dominance deviation exists within homozygous inbred strains. However, the accuracy of this estimate depends on the absence of variance from genetic interactions, which can not be guaranteed (Crusio, 1992). Note that the variance between inbred strains is divided in half because inbreeding results in the loss of intermediate heterozygotes, which produces a two-fold increase in genetic variation (Plomin and McClearn, 1993). Gene number The number of genes affecting brain weight in F2 intercross progeny can be estimated using the Castle-Wright formula: ( p1– p2)2/8VG ; where p1 – p2 equals the difference between the two parents and VG is equal to the phenotypic variance in the F2 intercross minus the phenotypic variance in the F1 (Wright, 1966). Modifying the formula to reflect the genetic variance among RI strains the equation for the number of effective genes among RI strains: D2/2V, where D is the difference between the highest and lowest strain mean and V is the variance of the RI strain means (Bailey, 1981). The accuracy of this computation relies on the assumptions of additive gene effects, unlinked genetic factors, polarized genetic factors in the parental strains (i.e. all increasing or decreasing alleles), and constant environmental effects. If these criteria are not met, the number of effective genes can be underestimated. At this stage, it is not possible to know if these criteria are met, and therefore the computations provide an estimate of the minimum number of effective genes. The number of genes involved in the variation of a trait can also be inferred from the phenotypic distribution of a segregating population.
Variation among strains, species and subspecies Average brain weights for 27 standard inbred strains range between 403 mg to 495 mg (Table 2.1). The average coefficient of variation (CV) for brain weight corrected with respect to sex, age and body weight within inbred strains is 3.9% and is 5.1% with the uncorrected brain weights. Brain weights for the wild Mus subspecies and species range from 303 to 454 mg, and the average CV for corrected brain weights is 4.5% and is 5.1% with uncorrected brain weights (Table 2.2). Note that the CV in the outbred strain CARL/ChGo is much higher 6.8%. The average phenotypic variance found within inbred strains is significantly less than the variance found between strains (F (24,323) = 49.7, p = 1.85E–93).
Table 2.1. Average brain weights for 27 standard inbred strains corrected for sex, age, and body weight.
*Pooled together 12 CBA/CaJ and 5 CBA/J mice
Table 2.2. Brain weight for Mus species and subspecies corrected for sex, age and body weight.
*outbred sample
The probability density distribution for 27 inbred strains has a platykurtic shape and kurtosis value of –1.0, indicating that there are many extreme values spread out over a wide range (Fig. 2.2). A platykurtic distribution implies the presence of two or more normally distributed populations with different means. The distribution is also positively skewed (+0.71), indicating that a disproportionate number of strains with high brain weights. Using the Kolmogorov-Smirnov goodness of fit test the inbred strain distribution was found to be significantly different from a normal distribution (p < 0.0001).
Figure 2.2. Probability density distribution of corrected brain weights for 27 inbred strains. The large shaded function represents a summation of individual probability densities for 27 inbred strains. The two small functions represent the strains LP/J with the lowest mean brain weight at 402.7 ± 18 mg and SM/J with the highest mean brain weight at 495 ± 14 mg. Brain weight means and SD were calculated from weights regressed with respect to sex, age, and body weight. The following probability density function was used to compute the probabilities:
In table 2.3, the column labeled d shows the differences between the F1 strain averages and their mid-parental values. The measure d estimates the net dominance effect of the genes on brain weight. The means of four F1 hybrids are close to their mid-parental values. The means of five F1 hybrids exhibit a slight to moderate dominance toward the high parental strain, while the brain weights of 32CASTF1 and CCASF1 exhibit overdominance. There was no significant difference in brain weight between the reciprocal F1 hybrids used to generate AC3HF2 and C3HAF2, although, there may be too few AC3HF1 cases for a reliable comparison. A significant difference was found between the reciprocal hybrids B6D2F1 and D2B6F1 (Difference (D) = 12.68 mg, t = –3.196, 26 df, p = 0.0036). The reciprocal B6D2F1 means are close to those previously reported by Seyfried and Daniel (1977). The average coefficient of variation for the F1 hybrids is 4.2%. This is not substantially less than that of the inbred strains and suggests that for brain weight the heterozygous state is not a significant buffer against environmental effects.
Table 2.3. Average brain weight for F1 hybrids and their parental strains
*Corrected F1 brain weights. Strains not corrected did not have significant effects from sex, age or body weight.
The CV for corrected brain weights is 6.8% between BXD strains and averages 3.8% within strains. The CV for corrected brain weights averages 4.9% in the intercrosses, and ranges from 5.5% in 32CASTF2, 4.6% in ABXD5F2, and 4.6 % in CCASTF2. The degree to which the brain weight CV were reduced by corrected weights varied from only 0.2% in AC3HF2/C3HAF2 to 3.2% in CCASF2. A significant difference in the variance between segregating and non-segregating generations is necessary to establish that genetic differences are responsible for brain weight variance. Using the variance ratio test, I examined whether brain weight variance in the recombinant crosses was significantly different from the pooled variance of their parents and F1 hybrid. The genetic variance in the ABXD5F2 cross is just barely significant at p = 0.05(F0.05 (1), 516, 65 = 1.33), while the genetic variance in 32CASTF2 is highly significant (F0.005 (1), 144, 69 = 1.75). The highly significance variance in the 32CASTF2 is expected considering the genetic diversity between the parental strains. In the AC3HF2 probability density plot, brain weight probabilities are slightly negatively skewed (Fig. 2.3). The probability density of CCASF2 is very narrow and indicates low brain weight variance within this cross. The probability density plots of AXB/BXA and 32CASTF2 appear platykurtic, where as, two modes are actually evident in the 32CASTF2 plot. Platykurtic distributions, especially those with two modes resolved, indicate that a small number of genes with large effects on brain weight are segregating within the cross. The location of the F1 function in the four intercrosses demonstrates partial or complete dominance, and, in the case of 32CASTF1 and CCASF1, overdominance.
Figures 2.3. shows probability density distributions of corrected brain weight for recombinant progeny and their parental strains. The variation in brain weight demonstrated in these graphs is independent of the covariance associated with body weight or other significant cofactor, such as age, sex, litter size, and parity. The large shaded function is a summation of individual normalized probability densities. Each individual function in an F2 distribution is derived from the corrected brain weight of one mouse and a standard deviation of 5 mg based on the estimated measurement error. In the RI distributions, the individual functions are derived from a strain mean and its SD. The thin black line is the function of the expected Gaussian distribution based on the mean and SD of the recombinant progeny. The smaller probability functions describe the mean and SD of parental strains. The BXD distribution includes 26 RI strains and the mean is 432 ± 30 mg (A). The AXB/BXA distribution includes 14 AXB and 14 BXA RI strains and the mean is 451 ± 20 mg (B). The mean of the ABXD5F2 distribution is 475 ± 21 mg (C). The AC3HF2 distribution includes both AC3H and C3HA and the mean is 454 ± 22 mg (D). The mean and SD of the CCASF2distribution is 439 ± 20 mg (E). The mean of the 32CASF2 distribution is 435 ± 24 mg (F).
The average brain weights in the intercrosses should equal the mid-parental values if brain weight is only under additive gene effects (Falconer and Mackay, 1996). From the F1 values, I anticipated the means for the 32CASTF2 and CCASF2 crosses to be above the mid-parental value, indicating dominance. While the 32CASTF2 mean did indicate dominance (d = 42), the mean of the CCASF2 cross was not well matched with the mid-parental value. This latter result is difficult to explain but could result from epistatic interactions being broken up during the segregation of the F2. Regression analyses Using multiple regression, brain weight was regressed with respect to the cofactors, sex, age, body weight, and fixation quality across inbred strains. Sex, age, and body weight all have significant effects on brain weight and together explain 44% of the variance in brain weight (Table 2.4). Body weight alone had the largest effect on brain weight, explaining 36% of the variance. No significant sex difference was found in absolute brain weight across strains (females: 451 ± 48, males: 453 ± 48). Male mice weigh on average 2.5 grams more than female mice, thus, when differences in body weight between the sexes are controlled for, females are significantly brainier, having on average an 11-mg heavier brain than males (Table 2.4). Brain weight is found to increases by almost 0.1 mg per day across strains and age differences can explain 5% of the variance in brain weight. However, when brain weight is controlled for with respect to body weight, brain weight relative to body weight decreases with age (Table 2.4). Fixation quality was assessed after dissection and the assigned score was used in a regression analysis to estimate the effects of fixation. The score was based on a five point scale: no fix = 0, poor fix (just post-fixed) = 1, marginal fix (just paraformaldehyde) = 2, adequate fix = 3, good fix = 4 and excellent fix = 5. Fixation quality had significant effects on brain weight. Brain weights were found to shrink by 2.4 mg for each increase in the fix quality rating.
Table 2.4. Inbred strain multiple regression analysis for brain weight.
*p = 0.0004, **p < 0.0001
A within strain regression analysis was performed in three strains (BALB/cJ, n = 61; C57BL/6J, n = 67; DBA/2J, n = 35). As expected, the effect of specific variables on brain weight differs between strains. In BALB/cJ and DBA/2J, body weight was an important variable, explaining 16.3% and 34.4%, respectively, while body weight was not a significant factor in C57BL/6J. There were no sex differences within any of these strains. While no age effects were found in DBA/2J and C57BL/6J, brain weight was found to increase by ~0.1 mg per day in BALB/cJ and explained 5% of the variance. Interestingly, no single factor had significant effects on brain weight in C57BL/6J. However, regressing sex, age, and body weight together explained 22% of the variance in brain weight in C57BL/6J, with body weight becoming significant only after being corrected with respect to sex and age. A regression analysis in the inbred wild strains demonstrated an age-effect similar to that found in the standard inbred strains, ~0.1 mg per day. However, age explained almost 10% of the variance in brain weight in wild strains, while the effect of body weight on brain weight accounted for only 10% of variance in brain weight. The body weights of the wild inbred strains are 40% less than that of the standard inbred strains, 14.2 ± 3.5 gm compared to 23.3 ± 6.8 gm.Among CCASF2 mice, variation in sex, age and body weight explains 52% of the variance in brain weight, with body weight accounting for the majority of the variance, 49.5% (Table 2.5). Absolute brain weight is significantly different between sexes (D = 19.48, t = –2.89, p = 0.0047, r2= 7.6%), however sex becomes an insignificant factor when body weight is controlled. Brain weight significantly increases with age in the CCASF2 cross, but after controlling for body weight, age becomes insignificant. Brain weight increased ~2 mg per day over the narrow age range between 30 to 55 days. In the CCASF2, variation in brain weight is significantly correlated with coat color. Coat colors were transformed into a numerical code, with the albino color given a 0, the light agouti a 0.5 and agouti a 1. The coat color coefficient of –12.41 in Table 2.5 indicates that brain weight decreases by 12.41 mg going from the albino–0 to the agouti–1. Thus, albino strains have a brain weight that is on average 12.4 mg heavier than the pigmented strains. A positive albino effect is expected since the BALB/cJ strain, which carries the albino allele, has the heavier brain weight. Differences in coat color explain only 3.1% of the variance in brain weight. Nonetheless, this is an important finding because it indicates that a gene modulating brain weight maps close to the gene tyrosinase on chromosome 7.
Table 2.5. CCASF2 multiple regression analysis for brain weight.
*p < 0.01; ** p < 0.0001
Among 32CASF2 body weight is the only significant factor influencing brain weight, explaining 13.6% of the variance in brain weight (Table 2.6). Absolute brain weight is significantly different between sexes in 32CASF2 (D = 10.53 mg, t = –2.45, p = 0.015, r2= 4.1%), however again, sex becomes an insignificant factor when body weight is controlled. There is no significant change in brain weight with age in this cross. A non-significant age coefficient does not necessarily mean that age has no effect on brain weight, but could rather reflect the narrow age range within the cross. The age range of 32CASF2 is from 30 to 54 days with the mode at 39 days. Data from this narrow of an age range may be insufficient to detect a gradual change in brain weight with age.
Table 2.6. 32CASF2 multiple regression analysis for brain weight.
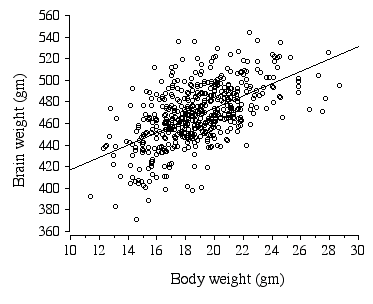
*p = 0.0004 In ABXD5F2 progeny sex, age, body weight, litter size, and parity all had significant effects on brain weight (Table 2.7). Body weight alone explains 32.2 % of the variance in brain weight (Fig. 2.4).
Table 2.7. ABXD5F2 multiple regression analysis for brain weight.
*p < 0.05, **p < 0.0001
Figure 2.4. Regression of ABXD5F2 brain weight and body weight .
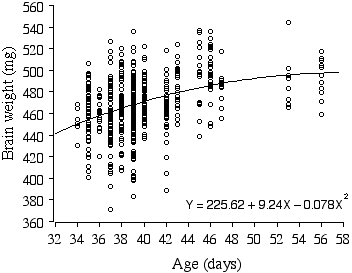
There is a small significant difference in brain weight between the sexes (D = 5.78 mg, t = –2.38, p = 0.01, r2 = 1.1%). Most remarkably, brain weights of the ABXD5F2 mice increase on average a whopping 2.4 mg per day, even within the narrow age range of 34–56 days, and explains 13.8% of the variance in brain weight (Fig. 2.5). When brain weight is regressed with multiple factors, age is still a positive factor, increasing brain weight on average by 0.69 mg a day! Note that the growth curve of ABXD5F2 brain weight in Fig. 2.5 appears to reach an asymptote around 48 days, suggesting that the preceding growth rate is an extension of the post-natal growth period.
Figure 2.5. Polynomial regression of ABXD5F2 brain weight and age.
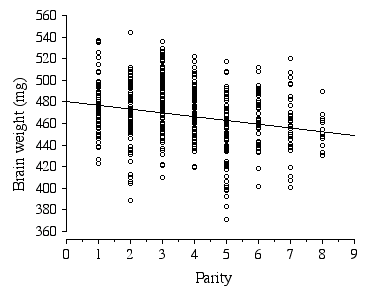
Litter size in the ABXD5F2 cross typically ranged between 5 to 15, with the average litter size being 10. Strikingly, the average brain weight of litters is stable over a 2-fold range in the number of pups per litter, 7 to 14 pups (F = 0.95, df = 46, p = 0.47). Only in the smallest (5 and 6 pups) and largest litters (15 pups) is brain weight affected. Parity, however, has a significant negative effect on brain weight, with brain weight decreasing by 2.4 mg with each successive litter (Fig 2.6). The parity effect persists even when the first and last litters were dropped from the analysis.
Figure 2.6. Regression of ABXD5F2 brain weight and parity .
To determine whether genetically identical ABXD5F1 mothers produce F2 offspring with significant differences in brain weight, I performed an analysis of variance, with the single factor being the identity of the mother. Litter averages for each of the eight dams were computed from individual brain weights corrected for differences in sex, age, body weight, litter size, and parity. The were no significant differences in the litter averages between dams, (F = 1.14, df = 8, p = 0.36). In AC3HF2 mice, sex, body weight, litter size, and parity all have significant affects on brain weight (Table 2.8). In C3HAF2 mice only body weight, sex and age significantly affect brain weight (Table 2.9). Body weight alone is responsible for 10% of the variance in brain weight in AC3HF2, but is responsible for 27% of the variance in C3HAF2. The polarity of the sex difference is different between AC3HF2 (D = 8.78 mg, t = 2.39, p = 0.01, r2= 4.2%) and C3HAF2 (D = 8.08 mg, t = –2.61, p = 0.01, r2= 3.0%). However, when body weight is controlled, the sex differences between crosses are closely matched, 22.5 mg and 19.8 mg. The reciprocal AC3HF2/C3HAF2 crosses are significantly different, with means and SD of 464.0 ± 21.4 mg and 458 ± 23.6 mg, respectively, (t = –2.53, n = 358, p = 0.01).The regression coefficients for two maternal effect variables (litter size and parity) also differ between the reciprocal AC3H/C3HA F2 crosses.
Table 2.8. AC3HF2 multiple regression analysis for brain weight.
*p < 0.05, **p < 0.01, ***p < 0.0001 Table 2.9. C3HAF2 multiple regression analysis for brain weight.
*p < 0.0001
In the BXD strains, body weight and age, are the only significant cofactors influencing brain weight (Table 2.10). Variation in body weight accounts for 17.4% of the variance in brain weight. The age of mice in the BXD strains ranged from 29 days to 444 days. Across all BXD strains, brain weight was found to increase by 0.16 mg per day, with variance in age explaining 2.5% of the variance in brain weight. The age-effect could be influenced by genetic differences, for example, if the individuals in the high brain weight strains were older. To eliminate genetic differences, I computed z-scores for individual brain weights based on the mean and SD within the strain. The age-effect with z-scores was significant and in fact, the effect was increased to 0.23 mg per day. There are no significant differences in absolute brain weight between sexes.
Table 2.10. BXD multiple regression analysis for brain weight.
*p < 0.01, **p < 0.0001
In the AXB and BXA strains, body weight explains most of the variance in brain weight, accounting for 35% of the variance in the AXB group and 27% of the variance in the BXA group (Table 2.11 and Table 2.12). There is no difference in absolute brain weight between sexes in AXB/BXA. Brain weight was found to increase significantly with age, equivalent to an increase of 0.28 mg per day. Since body weight also increases with age, controlling for body weight eliminates the age effect on brain weight. In the BXA strains, but not the AXB strains, there is a significant correlation between brain weight and coat color, (p = 0.0004). The coat coefficient of –15.85 indicates that albino strains have a brain weight that is on average 15.9 mg less than the pigmented strains. This effect is opposite to that found with the albino linkage in the CCASF2, but then a negative effect transmitted from A/J, which carries the albino allele, is expected since it has the lower brain weight. Coat color explains only 5.2% of the variance in brain weight. The reason a coat color correlation was not found in the AXB strains is because there are a disproportionate amount of pigmented strains in the set.
Table 2.11. AXB multiple regression analysis for brain weight.
*p < 0.05 **p < 0.0001
Table 2.12. BXA multiple regression analysis for brain weight.
*p < 0.01, **p < 0.001
Heritability and gene number The heritability of brain weight within inbred strains is 0.58. When minimizing the effects of variation in sex, age, and body weight on brain weight by multiple regression heritability of brain weight in the inbred strains is reduced to 0.51. The heritability of brain weight measured in the mapping crosses ranges from 0.15 to 0.39 (Table 2.13). The minimum number of genes modulating brain weight in these crosses ranges from one to six (Table 2.13).
Table 2.13. Heritability, brain and body weight correlation, and gene number for BXD, AXB/BXA, and F2 intercross mice.
*Hegmann and Possidente method
The significant difference in the variance of brain weight between and within inbred strains and the lower CV for brain weight within inbred strains (3.9%) compared to the outbred strain CARL/ChGo (6.8%) and F2 crosses (4.9%), demonstrates that genetic variation contributes to variance in brain weight across strains. The CV in inbred strains would probably have been lower had there been more environmental consistencies. For example, the CV in the heterogenous crosses are minimized by being sacrificed at nearly the same age, being reared in the same room, with many individuals born from the same parents and in some cases even coming from the same litter. In contrast, the individuals making up an inbred strain often vary widely in age, with some bred at the University of Tennessee while others were bred at The Jackson Lab. The probability density distributions demonstrate that brain weight is a complex trait influenced by multiple factors (Figs. 2.2 and 2.3). There are obvious differences in the genetic complexity between the crosses. The nearly bimodal distribution of the 32CASTF2 cross indicates that one to two genes have major effects on brain weight. The broad platykurtic distribution of AXB/BXA also suggests the segregation of a few major genes is modulating brain weight. The distributions reveal the genetic complexity of brain weight variation and indicate that there are genes with major effects on brain weight segregating among the inbred strains! Regression analyses Sex and brain weight. There was no difference in absolute brain weight between sexes within the inbred strains and in the BXD and AXB/BXA strains. This finding was unexpected since Roderick and colleagues had reported that the brains of females were on average 10 mg heavier than males (Roderick et al., 1973). Their analysis was based on a sample of 250 mice belonging to 25 inbred strains—17 of which I have also examined. When I examined these same 17 strains, I failed to detect a sex difference. Roderick and colleagues used retired breeders—animals that were probably older than 200 days. This discrepancy could be explained if a sex difference developed with increasing age. Indeed, an examination of the age effect between sexes within inbred strains revealed that brain weight increases in females by 0.06 mg more per day than in males and explained twice as much of the variance! However, dividing the sexes into groups, younger than 100 days and older than 100 days, still did not result in a significance sex difference in absolute brain weight. The increased age-effect in females could be related to the effects of sex hormones. For example, estrogen has been found to play a protective role in neurodegenerative diseases (Beyer, 1999). Recently, a study reported finding no difference in brain weight between the sexes in mouse, but did find a significant sex difference in rat (Bishop and Wahlsten, 1999). Incidentally, the mice in this study were young, 21-60 days, and the rats were older, 110 days. Brain weight in humans has been consistently reported to be higher in males compared to females (Pakkenberg and Gundersen, 1997; Peters, 1991). In conclusion, a difference in brain size between the sexes may not a universal phenomenon in mammals and should be investigated further with age-related changes in mind. There were absolute differences in brain weight between sexes in the crosses CCASF2, 32CASTF2, ABXD5F2 and AC3HF2/C3HAF2. The sex differences in these crosses suggest sex-specific influence on brain weight. A sex difference could result from the higher dosage of the X chromosome from one parental strain verses the other in the F2 females. The lower female brain weight, on average 5 to 10 mg less than males, is associated with a lower female body weight, on average 3 grams less than males. Thus, it is likely that the difference in brain weight results as pleiotropic effects from body weight factors during development. A body weight QTL accounting for 25% of the divergence between mouse lines has been mapped to chromosome X (Rance et al., 1997). Age and brain weight. A second important finding was that brain weight continues to increase with age in some mice even after reaching sexual maturity. Adult brain weight in mouse has been reported to reach its adult size by 2 weeks of age (Hahn et al., 1983; Kobayashi, 1963). However, in ABXD5F2 mice brain weight increased on average 2.4 mg per day between the ages of 34–56 days and in CCASF2 mice brain weight increased 1.1 mg per day between the ages of 29–55 days. In BXD and inbred strains, brain weight had a more modest increase, averaging 0.16 mg and 0.10 mg per day, respectively. In contrast, brain weights of 32CASTF2 and AC3HF2/C3HAF2 did not increase with age. Differences in the magnitude of the age effects between groups could be related to differences in the age range, e.g., the age range within inbred strains is much broader than in the F2 crosses. It should also be noted that the age effects within a narrow interval do not describe age effects at older ages. In the inbred strains, a large contribution of the age effect results from a high growth rate between 30 to 40 days. Dropping these cases reduces the explained variance by half. In contrast, brain weight in the BXD strains appears to occur linearly as a function of age. The differences between strains suggest that the mouse brain can have a persistent linear phase of postnatal growth that is genetically determined. In addition, a generality can not be made as to when the mouse brain stops growing, but as for body weight, brain growth is a continuum with inflection point that divides an exponential and linear phase. Why does brain weight increase with age? The ventricular volume in human brains increases with age (Celik et al., 1995), and an increased volume of cerebrospinal fluid within enlarged ventricles might increase brain weight. However, when brains from SM/J mice were dehydrated and weighed, the dry brain weight increased with age (personal communication from Robert Williams). It is not known whether the increase in dry brain weight results from glia proliferation, increased myelin content, or changes in mean cell size. Although one study reports that brain weight and DNA content in mouse remain constant from age 60 to 470 days (Howard, 1973), there has been no report of increasing brain weight past maturity in mouse. Numerous studies in humans have reported a reduction in brain weight and cortical neuron number with age (Flood and Coleman, 1988; Pakkenberg and Gundersen, 1997). Much of the decrease in brain weight in humans is associated with a decrease in white matter. In conclusion, an increase in brain weight with age in mice suggests that a decrease in brain matter is not a necessary consequence of aging. Body and brain weight. Variation in brain weight is associated with body weight among all animals studied. This correlation exists, both within strains, in which isogenic mice with heavier bodies tend to have heavier brains, and across strains, in which strains with heavier bodies tend to have heavier brains. In these mice body weight and brain weight is also highly correlated within the sexes. The correlation within strains is due to factors that affect the body and brain, such as maternal effects and parity. Contrary to mouse, brain weight in humans is not correlated with body weight within the sexes (Pakkenberg and Gundersen, 1997). In mouse, the correlation between brain and body originates during the embryonic and early postnatal period when the body and brain grows isometrically from a widespread circulation of growth-promoting factors (Riska and Atchley, 1985). For example, insulin growth factor (IGF)-I and -II are known to affect the growth of multiple organs including brain (D'ercole, 1993). Although IGF-I and -II are primarily synthesized within their target organs their expression is regulated by growth hormone, an endocrine hormone that is released from the pituitary and transported through the bloodstream. Thyroxine also circulates throughout the body during development and is known for its mitogenic effects in the brain and body (Morreale de Escobar et al., 1987). Litter size, parity, and brain weight. Litter size had a significant negative effect on brain weight in ABXD5F2 mice, explaining 9.4% of the variance in brain weight. However, when the extreme litter sizes were dropped, brain weight was stable across a two-fold range in litter size. In contrast, Wahlsten and Bulman-Fleming (1987) found litter size to have a highly negative linear effect on brain weight in study of 67 BALB/cJ litters ranging in size from 2 to 11 (Wahlsten and Bulman-Fleming, 1987). In another study, litter size explained 8% of brain weight variance found within inbred strains (Leamy, 1992). A study rearing rats in small and large litters found postnatal litter size to have a significant effect on brain weight (Sara et al., 1979). The effects of litter size could result from differences in postnatal nutrition as well as in utero nutrition. The stability of brain weight across litter sizes in the ABXD5F2 could be explained by the strong reproductive performance typical of F1 hybrids. The number of successive litters, or parity, was found to have a negative effect on brain weight. This result is not attributed to the small litter sizes occurring with the first and last parity, because when these litters were dropped parity still had a significant effect on brain weight. The effect of parity on brain weight could be related to the age of the mother, since parity and maternal age is highly correlated. It is conceivable that a decrease in the mother’s serum levels of brain growth-promoting factors, such as IGF-I, which occurs with progressing age in mice and humans, has repercussions on the developing fetal brain (Xu et al., 1995) (Klein et al., 1996) The regression coefficients and the amount of variance in brain weight explained by sex, age, body weight, litter size, and parity, differ between different groups of mice. Differences are even present between the reciprocal F2s from AJ and C3H/HeSnJ matings. Although the F1 hybrids have identical genomes, the X chromosome originates from two different strains in the reciprocal crosses—A/J and C3H/HeSnJ. Thus, differences between reciprocal crosses could result from sex-specific loci. In fact, there was a significant difference in brain weight between reciprocal F2 females (D = 13.9, t = –4.2, p < 0.0001, n = 193). There was also a large difference in the brain weight variance between reciprocal F2 females, (555 compared to 460 mg). However, a significant difference in brain weight was also found between reciprocal F2 males, albeit much smaller, although variance was alike in reciprocal males. Differences between reciprocal F1 males can also reveal the presence of a sex-linked trait. Unfortunately, there are too few reciprocal F1 males to make a reliable comparison. Differences between reciprocal crosses could result from maternal effects, such as cytoplasmic differences or genomic imprinting. In summary, the regression analyses demonstrate that body weight, age, sex, and parity, can explain a substantial portion of the variance in brain weight. Genetic variation The brain weights of F1 hybrids can reveal the cumulative additive or dominant action of brain weight QTLs. Genes with additive effects will combine in the hybrid and produce a mid-parental phenotype. This occurred in 4 of the 11 hybrids studied. When alleles are directionally dominant, the F1 hybrids will resemble one parent more than the other. Positive dominance occurred in 5 of the 11 F1 hybrids studied. When the phenotype of F1 hybrids exceed the phenotype of either parental strain there is overdominance. Overdominance was exhibited by two hybrids, CCASF1, and 32CASF1. It is interesting that both of these hybrids include CAST/Ei as the parental. These two F1 hybrids are from an inter-subspecific cross and demonstrate the effect of hybrid vigor or heterosis. Overdominance can occur when genes of the same polarity disperse among the parents and brought together in the F1 hybrid. In the case of CB6F1 note that both parents have high brain weights and that, the average brain weight for CB6F1 is higher than either parentals. The overdominance in CB6F1 could result if the parents had different genes with increaser alleles that behaved dominantly in the F1. The association of dispersed brain weight QTLs probably causes the ambi-directional dominance in two BXD strains (Table 3.1). The strain BXD5 has an average brain weight of 527 mg, while BXD27 has an average brain weight of 382 mg, both of these strains are more extreme than their parental strains. Overdominance can also result from epistasis, when alleles from two genes interact to produce a larger effect than their individual effects combined. Evidence that epistatis is involved in brain weight variation among mice comes from a study which found the generation means and variances from C57BL/6J and DBA/2J reciprocal crosses (backcross and intercross) were not adequately explained by an additive-dominance model (Seyfried and Daniel, 1977). The over-dominance exhibited in the F1 hybrids suggests that ancestors of these mice were subjected to selection pressures for high brain weight in the past and that brain weight must have been important for fitness at one time (Crusio, 1992). Genetic factors account for as much as 39% of the variation in brain weight in BXD strains and 51% in the inbred strains. This result is not surprising, given the number of studies that have reported genetics to be the major determinant of brain size (Bartley et al., 1997; Roderick et al., 1973; Wimer et al., 1969). Estimates of the number of genes producing variation in brain weight among the mice studied ranged from1 to 6. Together, the high heritability of brain weight and low gene number indicate that mapping a major brain weight QTL is feasible. Indeed the regression analysis with brain weight and coat color in the BXA strains and CCASF2 mice have tentatively located a brain weight QTL to chromosome 7, near the gene tyrosinase! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Neurogenetics at University of Tennessee Health Science Center
| Text Only | Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org