|
| |||||
|
| ||||||||
|
| ||||||||
Home  Publications Publications |
|
|
Note to the Reader Originally published in The Anatomical Record, Volume 94, pp. 239-247 (1946) by the Wistar Institute of Anatomy and Biology, Philadelphia, PA. Annotations by Robert W. Williams (1998). Last update by RW, 27 November, 2001.
Print Friendly
NOTE TO THE READER: Brackets [...] are used to denote annotations by
R. Williams. Brackets are also used to indicate page breaks so that
reference can be made to the original page numbers of the 1946
publication. [page 239 Top] Department of Zoology, The University, Birmingham, England Estimations of the numbers of nuclei in microtome sections are
frequently made in some branches of histology, particularly in the study
of endocrine glands, hemopoietic organs and the central nervous system.
The curious neglect of this and indeed of all quantitative methods in
most other fields of histology will no doubt soon be a thing of the
past. It is therefore important to consider how best to get reliable
conclusions from such nuclear counts. The present note deals with a
commonly neglected difficulty which necessarily follows from the use of
microtome sections. Although I confine discussion to cell nuclei, the
argument applies of course to any discrete component of tissue. The number of nuclei visible in a microtome section
1 can easily be counted. But not all of the objects thus
counted are whole nuclei. Some must be fragments of nuclei, because some
nuclei lie partly within the section examined, partly within an adjacent
section. It is impossible always to tell which are fragmentary, which
whole. One cannot therefore extrapolate from the mean apparent number of
nuclei within the volume of a microtome section to the mean number
within a cubic millimeter or a given mass of tissue without
exaggeration; since the count on a single section represents the [page
240] nuclear content of the neighboring tissue which contains the other
portions of the transected nuclei. Only if the average dimension of the
nuclei in the direction at right angles to that of the section is minute
in relation to the thickness of the section, will the exaggeration be
negligible. The bigger this nuclear dimension is in relation to section
thickness, the bigger the error, because the higher the proportion of
nuclear fragments. Agduhr (’41) clearly recognized this source of error.
Even if we work in an entirely relative way, and attempt to compare
the nuclear populations of different tissues, or of the same tissue
under different conditions, we may be led into error. For obviously any
difference in size of the nuclei in the tissues compared will by itself
lead to different counts. We can put these considerations more exactly as follows. The true
density of population, from which can be derived by simple proportion
the number of nuclei in any volume of tissue, is for our purposes best
regarded as the number of nuclear-points within unit volume. By a
nuclear-point I mean any geometrical point of the same relative position
in all nuclei; say midway along the dimension at right angles to the
microtome section. A nuclear-point cannot overlap two adjacent sections,
and the number of nuclear-points in a section can therefore be
extrapolated to the number in any volume of tissue without error, and
can serve for exact comparison of nuclear population in different
tissues. If P is the average number of nuclear points per section, A is
the crude count of number of nuclei seen in the section, M is the
thickness (in µ) of the section, and L the average length (in µ) of the
nuclei, then The derivation of this equation is explained in figure 1
[RW1]. It means that those nuclei whose nuclear-points are outside
the section but which are nevertheless represented, by fragments, inside
the section, have their nuclear-points extending through [page 241 top]
a volume of tissue of (on the average) the thickness of the mean nuclear
length. Since microtome sections are commonly roughly the same thickness
as the nuclear length, the error in extrapolating from A to the number
of nuclei per unit volume of tissue may often reach 100%. The error in
comparing on the basis of counts in sections two tissues whose nuclear
size is different is much less serious, since it follows from equation
(1) that a given change in L produces a disproportionately smaller
change in A when P is held constant
[RW2].
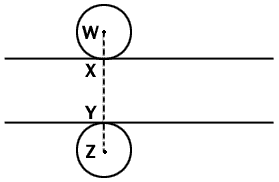
Fig. 1 Diagrammatic side view of a microtome section which
lies between the two lines. Two spherical nuclei of equal radius are so
place that they touch the surfaces of the sections at X and Y. Any
nucleus of this radius will be represented in the section if its center
lies anywhere between points W and Z. Since we can assume a random
distribution of nuclei between these two points, the proportion of all
the nuclei represented in the section whose centers lie within the
section is given by XY/WZ, that is section thickness/(section thickness
+ nuclear diameter). The argument applies statistically to nuclei of any
size or shape. The neglect of these considerations of nuclear size could be
illustrated by numerous examples. I have selected a few instances from
important papers of recent years. Kindred (’42) records many
differential cell counts made on sections of hemopoietic tissues,
without consideration of differences in nuclear size, and he apparently
extrapolates directly from section populations to populations of whole
tissues. Kirkman (’43) in his pioneering study of the cell composition
of kidney, compares fibrocyte and macrophage content of different
organs, and extrapolates from section counts to the whole organ,
apparently regardless of nuclear size. Kirkman [page 242] (’37), in
common with many other investigators of the pituitary, in comparing
relative numbers of different cell types in the pituitary under
different conditions makes no allowance for changes in nuclear size. He
records, it is interesting to note, a parallel increase in number and
size of basophils, and decrease in number and size of acidophils, after
gonadectomy. Clearly it is possible that the size changes account for
the numerical changes. Agduhr (’41) has criticised work on the central
nervous system, and I will not add any example in this field. Finally, I
wonder whether the size of mitotic figures is not sometimes relevant in
the very numerous investigations of mitotic rate. The neglect of nuclear size in these and similar papers may often be
harmless, but at least we ought to know that it is harmless. This can
only be achieved, and gross errors of extrapolation avoided, if we can
obtain the true density of nuclear, that is the density of
nuclear-point, populations of tissues. We need therefore a method of
obtaining the number of nuclear points in a microtome section. I here
suggest two methods, both of which I have used, in collaboration with
Dr. M. L. Johnson
[RW3], in a study of the nuclei of peripheral nerves (J. Anat. Lond.
in the press). If the average nuclear dimension at right angles to the plane of
section (hereafter called nuclear length) is known, the number of
nuclear-points within the section (P) can be obtained by means of
equation (1)
[RW4]. Rather surprisingly, a good approximation to the mean nuclear
length can be obtained in many tissues by measuring it directly in
sections cut at right angles to the plane of the sections counted. This
of course means that nuclear length has be measured on a sample of
tissue other than that on which the nuclear counts are done, and
sufficient material, homogeneous enough, must be available for this
[RW5]. The measurements of overall nuclear length are made, by micrometer
eye-piece, on a random sample of the apparent nuclei in the section.
Clearly the mean nuclear length so obtained must be less than the true
mean nuclear length because [page 243] we cannot differentiate whole
nuclei from shorter nuclear fragments. The mean length of all parallel
chords of a circle or of an ellipse (in the direction of one of the
axes) is 79% of the diameter (actually PI/4 X diameter, Dr. J. H.
Waterhouse informs me). It is probably an approximation adequate for
many tissues to treat nuclei as spheres or oriented ellipsoids, and we
might therefore expect a systematic error of about 21% when we measure
the mean nuclear length in sections of these tissues. We do not,
however, in practice measure this mean length, since the microtome
section is of finite thickness, and therefore, the full length of the
nuclei is disproportionately frequently included. If for instance we
consider spherical nuclei of average diameter 10 µ, whose length is
measured in sections 10 µ thick, the theoretical 21% underestimation is
halved. Furthermore, this 11% underestimate does not become translated
into an equivalent overestimation of the number of nuclear-points per
unit volume, as can be seen from equation (1). The error is in fact
nearly halved again, so that in our example the final overestimation of
density of nuclear-point population is only 6%. The value of L which, in
carrying out this method, we insert in equation (1) is really (assuming
nuclear shape as described) equivalent to L - (0.21T)/(T+N) L, where L
is the true mean nuclear length, N is the thickness of section in which
the nuclear lengths are measured, and T is the mean thickness of nuclei
(their dimension at right angles to these sections)[RW6].
The thicker the sections used for counts or measuring (the bigger M and
N), the smaller the error; the smaller either of the nuclear dimensions
concerned (L and T), the smaller the error. The error of overestimation
will in practice seldom exceed 10%. The 10% overestimation of population density is negligible for most
purposes, and it contrasts satisfactorily with the overestimation
resulting when no correction is made for nuclear size. If we are
primarily interested in comparing the density of population of two
tissues, we are on safer ground still, since the error in both densities
is in the same direction. [page 244] This method was used by Linderstrøm-Lang, Holter and Ohlsen (’35);
they did not discuss the size of the systematic error in getting nuclear
length from sections. Agduhr (’41) also described an analogous method,
which had been used by Carlson, Gustafsson and Möller (’37). Agduhr
likewise did not discuss the difficulties of obtaining nuclear
dimensions. He proposed a formidable formula by which the counts on
sections could be reduced to the true nuclear population. Since it may
lead to confusion we must briefly discuss his formula which was: This has been translated in the symbols used above, except that S
stands for the whole number of sections through or into which the
average nucleus extends. This formula is an approximation, since S is
always taken as a whole number. If S is made accurately equal to L/M,
then the formula simply reduces to equation (1)
[RW7]. Agduhr’s formula is therefore unnecessarily complicated,
though of course it gives valuable results. It is apparent from the preceding discussion that the nuclei
represented in any section consist of those whose nuclear-points lie
within the section (which we will call group A), and those whose
nuclear-points lie outside (group B). Group A gives us the true density
of population of the section; the size of group B depends on the average
nuclear length. If we compare the number of apparent nuclei we can count
in each of two consecutive sections of very different thickness, the
thicker section will of course contain more than the thinner. This is
because the number of group A nuclei is proportional to the thickness of
the section, though the number in group B is unaltered. The extra nuclei
added by thickening the microtome sections a given amount therefore at
once measures the true density of nuclear population. The procedure is to cut alternate sections at two thicknesses which
are as different as possible, consistent with the capacity of the
microtome and the difficulty of counting in [top of page 245] very thick
sections. Five and 12 µ are usually easily managed thicknesses. If 5 µ
and 12 µ are chosen, then the difference in the counts at these two
thicknesses is the number of nuclear points in 7 µ. The accuracy of the
microtome can conveniently be checked by the method of Marengo (’43).
If reliance is placed on comparing the nuclei per microscope field at
the two thicknesses, a difficulty may arise in that many microtomes will
not cut sections at different thickness which are of the same area
[RW8]. Though allowance can be made for this, there is bound to be a
sacrifice in accuracy. If possible it is far better to count all the
nuclei in the section, or in some morphological component of the section
(such as a funiculus of a nerve) which maintains a sufficiently contant
diameter through the section to avoid systematic error. The mean nuclear length, if this is of interest, can of course be
calculated from the counts at different thicknesses, since P, A and M in
equation (1) are known. It should be remembered however that the
apparent population is not a sensitive index of nuclear length, as
equation (1) indicates, so that accurate mean nuclear lengths cannot
easily be obtained. Method 2 allow the use of the convenient technique of Dornfeld,
Slater and Scheffé (’42) for getting the total volume of an organ. Their
graphical method for obtaining the number of cells in an organ can also,
with suitable modifications, be applied to method 2. It cannot be
accurately applied without method 2. Method 1 is on the whole less laborious, and though it involves a
systematic error this can be safely neglected in the majority of
investigations. Caution is however necessary in applying it to nuclei
which are not approximately spheres or oriented ellipsoids. The
correction for size of nucleus is not based on those nuclei which are
actually counted, and this may be a source of error; and the extra
tissue required for the measurement of nuclear length may not be
available at all. Furthermore, the measurements of nuclear length are
made in sections at right angles to those in which the nuclei are
counted; and since identification of cell [page 246] type may be
seriously affected by orientation of section (as it is for instance in
peripheral nerve) the correction of differential counts may be
impossible
[RW9]. Method 2 is more laborious, when large numbers of nuclei have to be
counted, and though theoretically accurate it probably involves in
practice an error of similar size to that of method 1
[RW10]. It can however be used on nuclei of any shape. It has the
great advantage that the true density of population is directly derived
from the counts. Extra tissue is not therefore required, and for
differential counting the work can be done in the plane of section in
which identification is easiest. I should like to thank Miss M. Bauer, Dr. M. L. Johnson and Dr. J. H.
Waterhouse for helpful discussion of these problems. SUMMARY The estimation of density of nuclear population and the accurate
comparion of the number of nuclei in different tissues, from microtome
sections, is only possible if size of nucleus is taken into account. Two
methods are described for doing this. LITERATURE CITED [Abercrombie, M., M. L. Johnson 1946 Quantitative histology of
Wallerian degeneration I. Nuclear population in rabbit sciatic nerve. J.
Anat. Lond. vol. 80, pp. 37-50.] Agduhr, Erik 1941 A contribution to the technique of determining
the number of nerve cells per volume unit of tissue. Anat. Rec., vol.
80, pp. 191-202. Carlson, Håkan, Dertil Gustafsson and Kjell L. Möller 1937 Quantitative,
mikromorphologische Studien über die Nebennieren einjähringer weisser
Mäuse unter besonderer Berückstichtigung von Geschlectsverschiedenheiten.
Upsala LäkFören. Förh., vol 43, pp. 49-82. Dornfeld, Ernest J., Daniel W. Slater, and Henry Scheffé 1942 A
method for accurate determination of volume and cell numbers in small
organs. Anat. Rec., vol. 82, pp. 255-259. Kindred, James E. 1942 A quantitative study of the hemopoietic
organs of young adult albino rats. Am. J. Anat., vol. 71, pp. 207-243.
Kirkman, Hadley 1937 A cytological study of the anterior hypophysis
of the guinea pig and a statistical analysis of its cell types. Am. J.
Anat., vol. 61, pp. 233-287. Kirkman, Hadley 1943 The number and distribution of macrophages and
fibroblasts in kidneys of albino rats with emphasis on 25-day males. Am.
J. Anat., vol. 73, pp. 451-482. [page 247] Linderstrøm-Lang, K., Heinz Holter and A. Søebord Ohlsen 1935 Studies
on enzymatic histochemistry. XIII. The distribution of enzymes in the
stomachs of pigs as a function of its histological structure. C. R. Lab.
Carlsberg, vol. 20, pp. 66-127. Marengo, Norman P. 1944 Paraffin section thickness—a direct method
of measurement. Stain Tech., vol. 19, pp. 1-10. Minor editorial corrections by Robert Williams (June 22,
1998): Since 11 August 98
|
Neurogenetics at University of Tennessee Health Science Center
| Print Friendly | Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org