|
| |||||
|
| ||||||||
|
| ||||||||
Home  Publications Publications |
|
|
Note to the Reader Please cite this work as: Williams RW, Gu J, Qi S, Lu L (2001) The genetic structure of recombinant inbred mice: High-resolution consensus maps for complex trait analysis. Genome Biology in press. This preprint accompanies the BXN RI dataset, release 1 of January 15, 2001
Print Friendly
Contents Introduction ABSTRACT Recombinant inbred (RI) strains of mice are an important resource used to
map and analyze complex traits. In this study we have increased the density
of microsatellite markers 2- to 5-fold in each of several major RI sets that
share C57BL/6 as a parental strain (AXB, BXA, BXD, BXH, and CXB). Genotypes
of more than 100 RI strains were extensively error checked and regenotyped.
A set of 490 markers that were typed in all constituent RI sets were used as
anchor loci to assemble high-resolution framework maps. The final consensus
maps are based on 1578 microsatellite loci and these maps have a cumulative
length of approximately 1400 cM after adjustment for recombination
frequencies of RI strains.
IntroductionRecombinant inbred (RI) strains have been used to map a wide range of
Mendelian loci and quantitative traits (Taylor, 1989). They offer compelling
advantages for mapping complex genetic traits, particularly those that have
low heritabilities. Each recombinant genome is replicated in the form of an
entire isogenic line (Bailey, 1981; Belknap, 1998; Crabbe et al., 1999; Toth
and Williams, 1999; Hain et al. 2000) and variance associated with
environmental factors and error can be suppressed to very low levels. This
effectively elevates heritability and greatly improves prospects for mapping
quantitative trait loci (QTLs). Recently, RI strains have also been used to
map QTLs that that are responsible for biometric variation in the
architecture of the mouse CNS (Belknap et al., 1991; Hitzemann et al., 1998;
Williams et al., 1998; Strom, 1999; Williams et al., 2000; Lu et al., 2000;
Airey et al., 2000). The main advantage in this context is that the complex
genetic and epigenetic correlations among interconnected parts of the brain
can be explored using complementary molecular, developmental, structural,
pharmacological, and behavioral techniques. Gene effects can also be tested
under a spectrum of environments and using numerous experimental
perturbations. RI strains can therefore be exploited to expose
gene-environment interactions. In contrast, interactions between genes and
the environment cannot usually be studied using conventional mapping
populations in which each animal is unique. Material and MethodsStrains and DNA. Genomic DNA for many strains was purchased from
the Jackson Laboratory (www.jax.org). DNA was obtained from 40 of 41 AXB and
BXA strains and 35 of 36 BXD strains, 12 BXH strains, and 13 CXB strains.
For visual clarity in this paper we have dropped hyphens and substrain
designations from RI strain names. For example, strain BXD-1/Ty is referred
to as BXD1. Databases and web-accessible data tables at www.nervenet.org
also use this simplified nomenclature. Formal strain and substrain symbols
of these strains are available at
jaxmice.jax.org/html/infosearch/pricelistframeset.html.
PCR Procedures Microsatellite loci distributed across all autosomes and the X chromosome
were typed using a modified version of the protocol of Love and colleagues
(1990) and Dietrich and colleagues (1992) described in detail at
www.nervenet.org/papers/PCR.html. A total of 1773 primer pairs (MapPairs)
that selectively amplify polymorphic MIT microsatellite loci were purchased
from Research Genetics (www.resgen.com).
Each 10 µl PCR reaction mixture contained 1X PCR buffer, 1.92 mM MgCl2, 0.25
units of Taq DNA polymerase, 0.2 mM of each deoxynucleotide, 132 nM of the
primers, and 50 ng of genomic DNA. Reactions were set up using a 96-channel
pipetting station. A loading dye (60% sucrose, 1.0 mM cresol red) was added
to the reaction before the PCR (Routman et al., 1994). PCRs were carried out
in 96-well microtiter plates. We used a high-stringency touchdown protocol
in which the annealing temperature was lowered progressively from 60 °C to
50 °C in 2 °C steps over the first 6 cycles (Don et al., 1991). After 30
cycles, PCR products were run on cooled 2.5% Metaphor agarose gels (FMC
Inc., Rockland ME), stained with ethidium bromide, and photographed. Gel
photographs were scored and directly entered into relational database files.
Common Markers. Databases. Relational database files were assembled from the
2000–2001
chromosome committee reports, the
Portable
Dictionary of the Mouse Genome (Williams, 1994, www.nervenet.org), and
the
MIT/Whitehead SSLP database Release 16. These files contain a summary of
information on chromosomal positions of over 6500 microsatellite markers and
information on an additional 20000 genes and markers. We have included
Nuffield Department of Surgery (Nds) microsatellite markers for which primer
sequences are available. Additional databases devoted to each RI set were
assembled from text files downloaded from the Mouse Genome Database. New and
corrected genotypes were entered directly into these files.

In general, we retained the order of microsatellite loci listed either in the Chromosome Committee Reports or in Releases 8 to 16 of the MIT/Whitehead microsatellite database. Markers were frequently reordered over short distances to maximize linkage LOD scores using the full BXN set. It is possible to reorder loci in single RI sets to obtain subset-specific improvements in LOD score, but this will introduce equal of greater numbers of recombinations in other members of the BXN set. Full genomic sequence data will soon make it possible to obtain definitive locus order and to fully integrate microsatellite maps with the physical maps of C57BL/6J chromosomes. Calculation of chromosome map lengths . We computed the total numbers of crossovers per chromosome to obtain an estimate of total chromosome length (Table 3). This procedure will be biased to the extent that double recombinantion events over short intervals are not detected. However, marker density is sufficiently high that the number of undetected recombinations is low. To compute the approximate length of intervals between adjacent makers we used an algorithm implemented in Map Manager QT. Map Manager QT counts all unambiguous recombinations in intervals between sequential markers. It then counts the number of crossovers that cannot be unambiguously assigned to a single interval due to incomplete marker data (Table 2). This second count is apportioned on a fractional basis to each interval in proportion to the number of unambiguous recombinations. The apportionment of ambiguously positioned crossovers is then recomputed iteratively until estimated numbers of crossovers converge to stable recombination fractions. Finally, Map Manager applies the Haldane-Waddington equation to calculate the equivalent recombination fraction for a single-generation cross. Error checking. To minimize genotyping errors we retyped a large
number of markers, particularly those that were associated with unusually
large numbers of recombination events. We were particularly interested in
minimizing the number of genotypes that appeared to be associated with two
closely apposed recombination events—what are sometimes referred to as
double recombinant haplotypes. These double recombinants appear to result
from two separate crossover events, one of which is just proximal to a
particular marker, the other of which is just distal to that marker. For
example the haplotype of a short chromosome interval, -B-B-B-B-N-B-B-B-B-,
is associated with two recombinations that flank the central marker with the
N genotype. Because of interference, the occurrence of two recombinations
within 10 cM is highly improbable in an F2 intercross and consequently,
double recombinants are often used estimate genotyping error rates or
incorrect marker order. However, recombination events accumulate over many
generations in an RI strain and interference is not a factor. Two or more
recombinations can be extremely close to each other and can produce true
double recombinant haplotypes. It is therefore necessary to verify all
apparent double recombinants in RI strains. We checked our own marker
genotypes and the majority of markers typed previously by other
investigators if they were associated with double recombinants in one of
more RI strain. When two or more strains contributed to double recombinants
we usually retyped all strains at that marker. Approximately 150 double
recombinant haplotypes (and 300 false recombinations) were eliminated in the
process of error checking. In a few instances our alternations have actually
generated new double recombinant haplotypes.
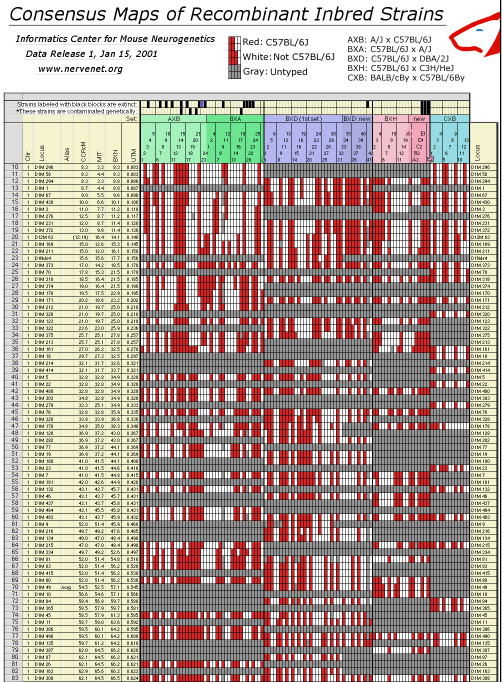
Results and DiscussionRI consensus maps of mouse chromosomesWhen we began this work fewer than 25 microsatellite markers had been
typed on each of the four major RI sets. We have increased this to 490
markers. We relied on these loci to assemble consensus RI maps. An
additional 986 MIT markers were typed by us and by other groups in at least
one set of RI strains. Any pair of RI sets share between 500 and 600 fully
genotyped markers. For example, the two largest RI sets—AXB/BXA and BXD—have
been typed at 591 common microsatellite markers. The RI maps are based on a
total of just under 1600 microsatellite makers (Table 2). The summed length
of all chromosomes (Chr Y excepted) is approximately 1413 cM when values are
converted from RI recombination frequencies to those expected of typical
single-generation maps. The corresponding Chromosome Committee Report (CCR)
maps have a cumulative length of 1494 cM between the same markers. The
MIT-Whitehead maps have a cumulative length of approximately 1384 cM. The
agreement at the whole genome level is excellent. Table 2. You may need to assign your browser more memory than usual to dowload this 9-meter-long "wall-paper" format figure in GIF image format. The original data files are also avaiable in standard text format. Column definitions from left to right: Chr: chromosome assignment based on BXN data set. Our assignments differ in a number of cases from those of the Chromosome Committees. Locus: an abbreviated version of the locus symbol. To improve legibility we have truncated D1MitNN to D1M NN. CCR cM: the position of the locus given in the most recent chromosome committee reports (2000 or 2001), MIT: the position of the locus given in databases at the Whitehead Institute, BXN: The position computed from the current RI dataset adjusted for map expansion, UTM: whole genome position in Morgans with a 5 cM buffer between chromosomes. This UTM column can be used to construct whole-genome LOD score plots. Opening this GIF file in Photoshop requires approximately 100 MB of RAM.
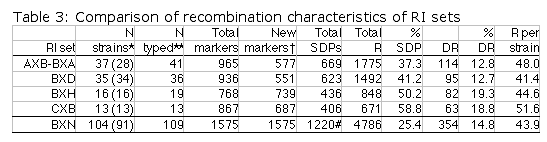
Table 3 column definitions: Total SDPs is the total number of unique
strain distribution patterns identified in each set. Total R is our
estimate of the total number of independent recombinations represented in
each complete set of RI strains including members of RI sets that are now
extinct. %SDP is our estimate of the percentage of the total number of
SDPs that have actually been identified in association with particular
markers. This number was computed by dividing "Total SDPs" by "Total R +
20". DR is the sum of recombinations associated with double recombinant
haplotypes in each RI set. %DR is the percentage of recombinations
associated with these double recombinant haplotypes. R per strain is the
estimate of the average number of recombination events accumulated by
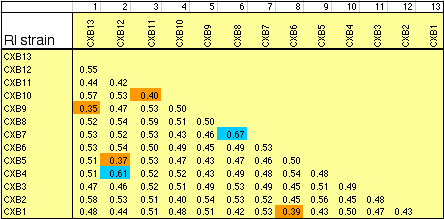
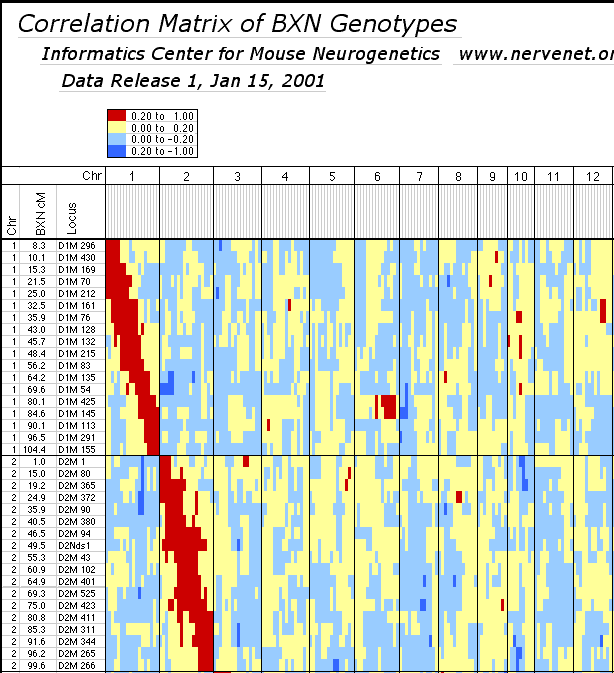
individual RI strains. Strain independence. Several RI strains share common haplotypes and recombination breakpoints. This duplication or non-independence of RI lines will distort genetic maps. To systematically search for and eliminate partial duplicate RI lines we constructed a genotype similarity matrix for all strains using Qgene (Nelson, 1997). An example of a small part of this matrix is illustrated below for the CXB set.
As already noted by Sampson et al. (1998), three sets of AXB and BXA strains show high genetic similarity:
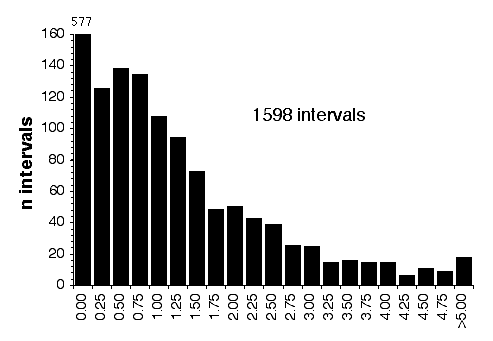
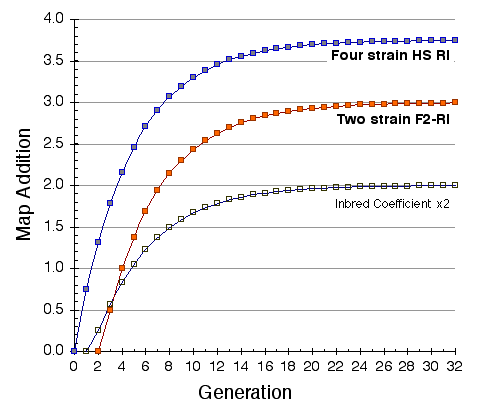
Map lengths. The mean frequency of recombinations CRI between two linked markers in an RI strain generated by breeding siblings is approximately 4c/(1+6c) were c is the recombination fraction per meiosis (Haldane and Waddington, 1931; Lynch and Walsh, 1998, p 436). An infinitely dense RI map should therefore average four times the length of the conventional one-generation F2 map. Most expansion is achieved in the first few generations, and by F7 the genetic map is approximately three times the length of an F2 map (Fig. 3). The expectation is that a map based on loci spaced at intervals of 1 cM (c = 0.01 in an intercross of backcross) will be expanded approximately 3.66-fold. Similarly, a low-density map based on markers at 16 cM will appear to be expanded 2-fold. F2 and N2 maps generated using uniform typing procedures typically have a cumulative length of 1300 to 1400 cM. Five conventional crosses that we have generated (four F2s and one N2, each genotyped at 91 to 128 loci) average 1320 ± 50 (SEM) cM in length. In comparison the fully error-checked native BXN map is approximately 3.6- to 3.7-fold longer, or a total of 4786 cM. The expansion averages approximately 3.4-fold when the comparison is made to the CCR consensus maps (Table 4). The expansion between common proximal and distal markers ranges from 2.8 in Chr 5 to 3.8 in Chr 12. In general the expansion estimate of 3.6–3.7 agrees extremely well with the Haldane-Waddington expectation given a mean spacing between neighboring markers of about 2–3 cM. The X chromosome only recombines with half the frequency of the autosomes and for this reason its expansion is only 1.8 fold.
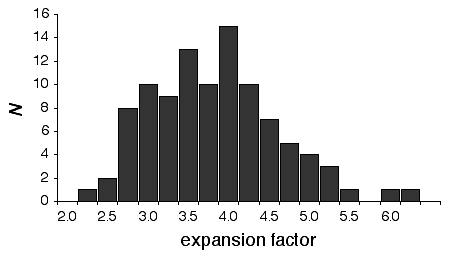
There is considerable variation in the average expansion among strains: from a low of 2.24 in BXD40 (the RI strain with the fewest recombinations) to a high of about 6 in BXH6 (Fig. 3). The highly recombinant RI strains will typically be more useful in mapping traits. It would be advantageous to generate RI lines from animals that are more highly recombinant than an F2 generation. By genotyping and selectively breeding more highly recombinant animals it would be possible to generate RI strain sets that significantly exceed the expansion predicted by the Haldane-Waddington equation. A 6x to 8x map should be attainable. Recombination density can also be increased by starting an RI strain using either advanced intercross progeny or heterogenous stock (Fig. 3). Recombination events accumulate additivity across generations and crosses. It is tempting to think that an advanced intercross with a 4x map expansion when used to generate a set of RI lines will experience an additional 4x expansion, or 16x total. This is incorrect. The total expansion of an RI line derived from an 8th generation advanced intercross will be close to 8x if matings are random. Figure 4 Mean expansion of the genetic map in RI strains. The average is approximately 3.7 for 100 independent RI lines. The X axis can also be considered the mean number of recombinations per 100 cM in different RI strains. The x axis can also be transformed into the total number of recombinations per strain by multiplying by the genetic length of the mouse genome in morgans (approximately 14 Morgans; 2.25x = 31.5 recombinations/strain, 3.00x = 42 recombinations/strain, 4.0x = 56 recombinations per strain; and 6.00x = 84 recombinations per strain).
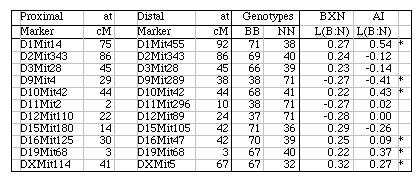
Strain distribution patterns. We concentrated genotyping efforts on intervals with comparatively low densities of fully typed microsatellite markers or that appeared to harbor large numbers of recombinations between neighboring markers. Our goal in generating a dense map was to discover and verify as many strain distribution patterns (SDPs) as possible in each RI set given available microsatellite primer pairs. The total number of SDPs in each RI set is approximately equal to the number of recombinations defined by a very dense map. Individual RI strains contain an average of 47 recombinations with a range that with few exceptions is between 40 and 60. The 13 CXB strains are associated with a total of 671 recombinations, whereas the set of BXD strains are associated with approximately 1492 recombinations, or just over one recombination per centimorgan on a standard F2 intercross map. These estimates are systematically deflated by a failure to discover recombinations in still sparsely mapped regions (regions where c is as high as 0.1) but are inflated by typing errors and errors of marker order. Based on current marker density we estimate that we have defined from 35% (AXB/BXA) to 59% (CXB) of the total set of SDPs (Table 1). To discover 406 (59%) of the 671 SDPs in the CXB set required 862 selected markers. Recovering the majority of the remaining 300 SDPs could require an additional 500 well placed makers. However, only the small number of strains that have recombinations actually need to be genotyped to fill SDP gaps. The density of informative microsatellite markers is not yet dense enough to define many more SDPs in the BXN set, but once microsatellite maps have been integrated into chromosome sequence databases it will be straightforward to generate additional single nucleotide polymorphisms and microsatellite markers and use them to define all 5000–6000 SDPs in the BXN set. It will then also be possible to refine the positions of recombination breakpoints. To define the remaining SDPs will be an extremely useful addition for mapping both Mendelian and quantitative traits. Locus order. The order of loci of the BXN consensus map generally conforms to that of the chromosome committee reports and the MIT-Whitehead genetic maps (Table 2). In about 130 instances we have changed the local order of loci over short intervals. For example, D1Mit276 and D1Mit231 on proximal Chr 1 do not recombine in the MIT F2 cross, but in the BXN set there is a single recombination between these markers in BXA11 that is most consistent with a reversal of order relative to the chromosome committee report (compare the columns lableled CCRcM, MITcM, and BXNcM in Table 2). The only non-trivial discrepancy was on proximal Chr 15. We reordered approximately 32 loci of Chr 15 to improve linkage statistics. We have not attempted to integrate the BXN data with numerous other mapping panels and it is likely that CCR order will often be well supported by either large mapping panels or rapidly improving physical maps. Full sequence data will soon resolve these minor inconsistencies. Segregation distortion and Hardy-Weinberg equilibrium expectation of allele fixation in RI sets. In the absence of selection approximately 50% of the strains should have inherited B alleles at each marker. A chi-square statistic can be used to assess whether a particular marker has an observed segregation ratio of B and N alleles that differs significantly from expectation. Only the 11 intervals listed below have chi-squared values that are significant at the 0.01 level. Eight of 11 intervals are biased in favor of B alleles. This is most extreme on chromosomes 1, 15, and X, where there are about twice as many strains with B alleles as N alleles. The opposite pattern is seen on chromosomes 9, 11, and 12. Given the large number of comparisons many instances of distortions may be type I statistical errors. We recently genotyped a tenth-generation advanced intercross between C57BL/6J and DBA/2J and it is therefore possible to test whether similar distortion patterns are present in this multigenerational cross. The short answer is that the fixation patterns seen in the BXN are replicated in 6 of 11 intervals. The correlation between ratios of alleles (log of B/N) in these intervals was positive (r = 0.41). It is likely that several of the intervals marked in Table 5 with asterisks represent regions that harbor polymorphic loci that affect fitness. Table 5: Hardy-Weinberg deviations in the BXN Non-syntenic associations. One important issue in using RI strains for mapping complex traits is that intervals on different chromosomes can become tightly associated or linked in a statistical sense. This non-syntenic association can arise either as a result of random fixation of alleles on different chromosomes during the production of RI strains or can arise as a result of selection for particular combinations of alleles on different chromosomes. Similar patterns of non-syntenic disequilibrium are common in recently admixed human populations and often lead to false positive signals when mapping complex traits. In mice even a modest selection coefficient expressed over 10 generations of inbreeding can generate positive and negative non-syntenic disequilibrium throughout the genome. For example if the combination of B alleles on distal Chr 1 and B alleles on proximal Chr 19 is favorable for fitness then two these intervals will effectively be in linkage disequilibrium in the final RI set. Disequilibrium can also take on the form of strong negative correlations and B alleles may be associated strongly with the group of N alleles. We searched for marked deviations from Hardy-Weinberg two-locus equilibrium by making a series of large correlation matrix of SDPs of pairs of markers. This was done for the entire BXN set and for the constituent RI sets. Table 6 summarizes the most extreme positive and negative correlations among the composite set of 102 independent BXN RI strains. Whether due to chance fixation, selection and epistasis, non-syntenic associations of the sort illustrated in Table 6 are a major source of both false positives and negatives in using RI sets and it is important to examine the correlation matrix once a set of QTLs have been provisionally mapped to see how there summed effects of multiple QTLs disequilibrium will produce spurious QTLs in regions not actually associated with trait variance.
Controlling for non-syntenic association. Associations among non-syntenic loci can be computed in advance of QTL mapping. It is possible to statistically control for these built-in genetic correlations when mapping by comparing the phenotypes to "residual" genotype values in which non-syntenic linkage has been controlled in a way similar to composite interval mapping. For example, in Table 6 the genotypes at marker D1Mit83 can be partly predicted by genotypes at markers on Chr 7 and Chr 10. D1Mit83 is treated statistically as a dependent variable and markers on Chr 7 and 10 are used as predictors. The residual genotype at D1Mit83 is subsequently used for QTL analysis. Unlike composite interval mapping, the set of controlled loci will vary for each marker and interval. Controlling for non-syntenic correlations will reduce Type I error, but there may be a significant regional loss of power. The process of controlling will introduce blind spots in the genome scan. Intervals that can be almost entirely predicted by combinations of other non-syntenic intervals will effectively be eliminated from a mapping study and QTLs in those intervals may be missed. For this reason it is essential to perform each scan both with and without control for non-syntenic association. The odd situation may arise that a single QTL will need to be assigned initially to two or more physically unlinked chromosomal intervals. Residual heterozygosity. In theory a set of 75,000 genotypes
generated across the genome of 100 RI strains should detect only a single
residual heterozygous loci at F55 (Fig. 2, fine line; the inbreeding
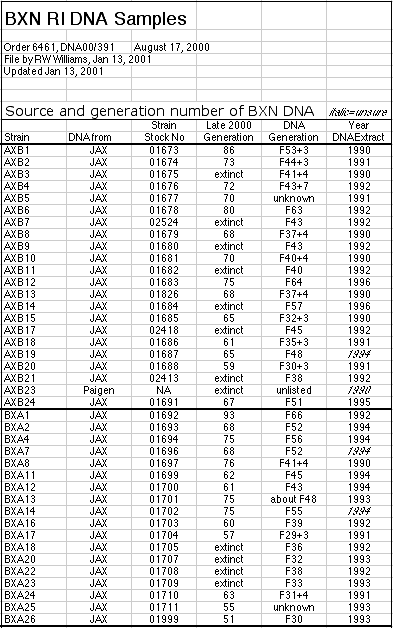
coefficient at F55 is 0.99998812). DNA from most lines was extracted in the
1990s at F generations between F20 and F70 (see Methods and Materials). We
detected a total of 10 intervals in nine strains that are heterozygous. Four
of these 9 strains are now extinct (BXA20, BXD37, AXB21, and BXA23). DNA
samples were taken from single animals of each strain and for this reason
these estimates of residual heterozygosity underestimate the total
heterozygosity about twofold.
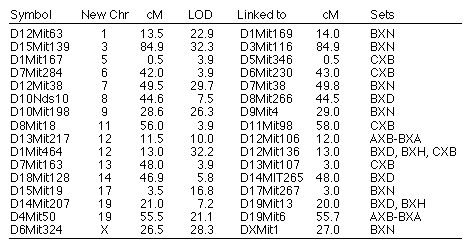
Reassigned microsatellite loci. A number of microsatellite loci
map to locations on chromosomes other than those expected on the basis of
their original assignments (Table 7). Mapping data in one or more of the RI
sets is consistent with a reassignments for 16 microsatellite loci to
different chromosomes. All of these reassignments are provisional,
particularly those with LOD scores less than 10. In several cases, (e.g.,
D10Nds10) we have reassigned microsatellite loci typed by other
investigators that now are linked to new and firmly mapped markers. All
primers used to amplify these microsatellites (D10Nds10 excepted) were
resynthesizing to confirm that they are identical to those originally
specified by Dietrich and colleagues.
CommentarySynopsis The analysis of complex traits using recombinant inbred (RI) strains has been hampered by the modest number of RI strains. Fortunately, five of the most widely used sets of RI strains share C57BL/6 (B) as a parental strain, and it is useful to pool these sets to generate a BXN superset consisting of approximately 100 RI lines. To simplify the use of the BXN set we have increase marker density in all RI lines and have merged the sets using a framework based on 490 shared markers. Approximately 1000 unique strain distribution—an average of almost one per 1.5 cM were discovered and mapped. The cumulative RI map is about 5000 cM in length, or roughly 3.6 times the length of standard intercross or backcross maps. When corrected using the Haldane-Waddington equation the RI maps have a cumulative length of 1400 cM. Information content of RI strain sets Despite the accumulation of genotypes in RI strains, these genetic resources have still not been typed with sufficient density to accurately define the frequency and positions of recombination breakpoints—to extract the most information from the strain resources. In the venerable set of 13 CXB strains only 11 unique SDPs had been assigned to Chr 1. With a more dense map that is now based on approximately 60 markers we have recovered at total of 37 recombinations on Chr 1, approximately 3 recombinations per strain. The positions of these recombinations has been defined with a precision that ranges from 0.5 to 6.0 cM intervals (2.3 cM average) as referenced to standard CCR maps. Twenty-one of the 38 SDPs are represented by one or more of the marker genotypes, but at least 17 SDPs remain to be defined and these SDP unfortunately cannot be predicted unambiguously. For example, if neighboring markers P and D have the genotypes BBCCC and CCCCC, then there must be at least two recombinations between the markers and there must be at least one unrecovered SDP. We do not know whether the intercalated SDP is BCCCC or CBCCC until we actually type markers in the P–D interval. To discover the missing SDP may require considerable effort especially if available polymorphic markers on the P–D interval have been exhausted. All unrecovered SDPs lower the information content of an RI set. Their absence can significantly reduce linkage of both Mendelian and quantitative traits that are unlucky enough to be controlled by loci in the intervals with ambiguous SDPs. How dense a marker map would be required to define more than 90% of the total number of strain distribution patterns? With 862 markers we were able to define approximately 60% of all likely SDP among the 13 CXB strains. However, in the collected set of BXN RIs only about 25% of the estimated 5000 SDPs have be defined with MIT microsatellites. We can estimate the density of the marker map that would be necessary to define 95% of the SDPs. For example for the BXD set if one assumes a random and independent distribution of breakpoints across strains and a random distribution of markers it would take a map with about 2,700 markers to define 95% of the 1,536 SDPs. Fortunately, the genotyping can be carried out systematically with efforts only directed at intervals very likely to harbor breakpoints. The precision of the maps can be improved in stages with progressively less genotyping in second and third rounds. However, it will be necessary to have access to highly polymorphic makers in critical intervals. Full sequence data of C57BL/6J will make it possible to extract comprehensive lists of polymorphic di- and trinucleotide repeats that can then be rapidly screened. Once QTLs have been mapped to candidate intervals, the subset of strains with recombinations within those intervals become an important resource for confirming and refining QTL location (Darvasi, 1998). This is especially the case if one exploits the RIX method devised by David Threadgill and colleagues. For QTLs or other loci that have already been mapped to a particular chromosome it is useful to have a list of strains in order of their information/recombination content by chromosome. This information can be easily extracted from Table 2 in order to make the appropirate set of RIX F1 intercross progeny to test and refine QTL location. The Potential Power of a QTL Consoritum and Rejoinder to the Commentary in Nature Genetics by Nadeau and Frankel. [Note: This section is an adapted version of a letter by RWW dated Aug 15, 2000.] An important issue is where effort and funding is going to be placed in mouse functional genomics in the next few years. Many geneticists, the DOE, the NIH, and the European mouse genetics community now strongly support large-scale mutagenesis screens. Many researchers are simultaneously involved in complementary QTL studies of specific biologically and clinically important traits. Although QTL research is fairly well supported, this support is distributed widely in the form of smaller grants, and there are currently (2001) no large-scale collaborative QTL programs that match ongoing mutagenesis programs in scope or scale. This as a missed opportunity to build on the strength and expertise of the rapidly expanding international mutagenesis program. After the commentary in Nature Genetics by Joe Nadeau and Wayne Frankel (2000), it may be helpful to reemphasize some of the positive features of QTL analysis. It is also worth redirecting their more pessimistic assessment by pointing out possible solutions to problems they raised, emphasizing how QTL analysis and mutagenesis can work together to increase the yield of genes with known functions. QTL analysis and ENU mutagenesis are both ways to isolate weak alleles that modulate traits. If all we expected of mutagenesis were knockouts or overexpressing lines, we could generate them directly by transgenesis and skip much of the front-end work. QTL analysis has the significant advantage of being targeted at specific biological problems and traits. It also has a somewhat predictable yield of loci per number of genotypes that are phenotyped. All of the massive phenotyping and bioinfomatics skills that are now being applied to mutagenesis can be applied with equal force to systematic QTL analysis. A problem of QTL mapping is that initially stages of analysis are well suited for small research groups (hence, the current R01 structure of support), whereas the later stages of QTL cloning are not (hence, the current frustration of many in this field). High precision QTL mapping requires resources that are not generally available to individual investigatorsÑlarge colonies, high-throughput phenotyping, and significant genotyping requirements. QTL cloning is not an oxymoron, but to prove it, mouse quantitative and molecular geneticists will need to collaborate much more effectively and on a larger scale than we do now. We also need to develop specific genetic resources that will permanently reduce both genotyping and phenotyping burdens. Along these lines, my suggestion is to generate (and expand) several very large sets of recombinant inbred (RI) strains with the goal of producing several sets each with an average map resolution of less than 0.25 cM. This level of resolution would require about 200 conventional RI strains (RIs derived from F2s) or about 50 to 80 advanced RI strains (RIs made from an advanced intercross progeny). Three to six complementary large sets of RIs would allow different QTLs to be harvested for single traits. Each RI set should ideally incorporate more than 6000 breakpoints, giving an average of less than 500,000 base pairs between breakpoints across all autosomes. Generating, genotyping, and phenotyping these strains would require a level of effort equivalent to that of a large mutagenesis project. The RI resources would be permanent and would require relatively modest long-term upkeep given the genetic payback. All data would be cumulative, results could be readily confirmed or refuted, genetic architecture could be explored easily, and even difficult genetic problems, such as norms-of-reaction, maternal effects, and epistasis, could be studied using massive RI intercrosses (RIX). A set of 50 RIs can be converted into 1225 RIX F1s. Combining large RI sets with complementary consomic sets, such as those being made by Joe Nadeau and colleagues, would allow rapid identification of QTLs (using the consomic lines), followed by rapid fine-mapping using the RI and RIX lines. If one wanted to, one could finesse the reciprocal congenic step altogether. The objective of this type of QTL mapping and cloning is the discovery of sets of polymorphic genes associated with well-defined biologically and clinically important heritable traits. The ultimate targets of complex trait analysis are networks of molecules modulated by the polymorphic QTLs, not just the QTL genes individually. There is significant amplification at this stageÑeach QTL is a potential handle on many interacting molecules. It might "only" take 5000 QTLs to get at 50,000 genes. Compared to a reduced "one gene-to-one phenotype" model, complex trait analysis is a somewhat more pragmatic way to think about gene function and the statistical association between alleles and traits.
AcknowledgmentsThis research project was support by a grant from the National Institute of Neurological Disorders and Stroke (R01 NS35485) and as part of the Informatics Center for Mouse Neurogenetics, a Human Brain Project/Neuroinformatics program funded jointly by the National Institute of Mental Health, National Institute on Drug Abuse, and the National Science Foundation (P20-MH 62009). The authors thank Dr. Xiyun Peng for her assistance in genotyping CXB and BXH mice. The authors thank Research Genetics and Ms. Felisha Scruggs for resynthesizing 18 MapPairs for us. We thank Susan Deveau of the Jackson Laboratory DNA Resource for information on the generation numbers of RI DNA samples. We thank Drs. David Threadgill, Gary Churchill, and Kenneth Manly for comments on this preprint.
Data Files: Text, Excel, and Image formatTwo types of key data are included in the list below in various formats. Items 1 through 4 are versions of the BXN genetic maps and microsatellite marker genotypes. Item 5 includes several different files that present the two-locus correlation matrices of genotypes for different subsets of strains. These correlations matrices are used to detect unsuspected associations between loci on different chromosomes (see main text for an explanation of Non-syntenic Association and the use of the matrices).
ReferencesAirey DC ,Lu L, Williams RW (2001). Genetic control of the mouse
cerebellum: identification of quantitative trait loci modulating size and
architecture. Journal of Neuroscience, 21:5099–5109.
Bailey DW (1959) Rates of subline divergence in highly inbred strains of mice. J Heredity 50:26–30. Bailey DW (1981) Strategic uses of recombinant inbred and cogenic strains in behavior genetics research. In Genetic research strategies for psychogiology and psychiatry. Gershon ES, Matthysse S, Breakefield XO, Ciaranello ED, eds. Plenum NY pp 189–198. Belknap JK (1998) Effect of within-strain sample size on QTL detection and mapping using recombinant inbred strains of mice. Behav Genet 28:29–38. Caldarone B, Saavedra C, Tartaglia K, Wehner JM,Dudek BC, Flaherty L (1997) Quantitative trait loci analysis affecting contextual conditioning in mice. Nature Genetics 17:335–337. Churchill GA, Doerge RW (1994) Empirical threshold values for quantitative trait mapping. Genetics 138:963–971. Darvasi (1998) Experimental strategies for the genetic dissection of complex traits in animals. Nat Gen 18:19–24. Dietrich WF, Katz H, Lincoln SE (1992) A genetic map of the mouse suitable for typing in intraspecific crosses. Genetics 131:423–447. Don RH, Cox PT, Wainwright BJ, Baker K, Mattick JS (1991) ÔTouchdownÕ PCR to circumvent spurious priming during gene amplification. Nucleic Acids Res 19:4008. Hain HS, Crabbe JC, Bergeson SE, Belknap JK (2000) Cocaine-induced seizure thresholds: quantitative trait loci detection and mapping in two populations derived from the C57BL/6 and DBA/2 mouse strains. J Pharmacol Exp Ther 293:180–187. Haldane JBS, Waddington CH (1931) Inbreeding and linkage. Genetics 16:357–374. Haley CS and Knott SA (1992) A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69:315–324. Laird PW, Zijderveld A, Linders K, Rudnicki M, Jaenisch R, Berns A (1991) Simplified mammalian DNA isolation procedure. Nucleic Acids Res 19:4293 Love JM, Knight AM, McAleer MA, Todd JA (1990) Towards construction of a high resolution map of the mouse genome using PCR-analyzed microsatellites. Nucleic Acids Res 18:4123–4130. Lu L, Airey DC, Williams RW (2001) Complex trait analysis of the mouse
hippocampus: Mapping and biometric analysis of two novel gene loci that
modulate hippocampal size. Journal of Neuroscience, 21:3503Ð3514.
Lynch M, Walsh B (1998) genetics and analysis of quantitative traits. Sinauer Associates, Inc. Sunderland, MA. Nelson JC (1997) QGENE: software for maker-based genomics analysis and breeding. Molec Breeding 3:239–245. Panoutsakopoulou V, Spring P, Cort L, Sylvester JE, Blank KJ , Blankenhorn EP (1997) Microsatellite typing of CXB recombinant inbred and parental mouse strains. Mamm Gen 8:357–361. Routman E, Cheverud J (1994) A rapid method of scoring simple sequence repeat polymorphisms with agarose gel electrophoresis. Mamm Genome 5:187–188 Sampson SB, Higgins DC, Elliot RW, Taylor BA, Lueders KK, Koza RA, Paigen B (1998) An edited linkage map for the AXB and BXA recombinant inbred mouse strains. Mamm Gen 9:688–694. Taylor BA (1989) Recombinant inbred strains. In (Lyon ML, Searle AG, eds) Genetic variants and strains of the laboratory mouse 2nd Ed Oxford UP, Oxford. pp 773–796. Taylor BA, Wnek C, Kotlus BS, Roemer N, MacTaggart T, Phillips SJ (1999) Genotyping new BXD recombinant inbred mouse strains and comparison of BXD and consensus maps. Mamm Gen 10(4):335–348. Darvasi (1998) Experimental strategies for the genetic dissection of complex traits in animals. Nat Gen 18:19–24. Weber JL, Broman KW (2000) Genotyping for human whole-genome scans: past, present, and future. Adv in Genet 42:77–96. Williams RW (1998) Neuroscience meets quantitative genetics: Using morphometric data to map genes that modulate CNS architecture. In: Morrison J, Hof P (eds) Short course in quantitative neuroanatomy. Society of Neuroscience, Washington DC, pp 66—78. Williams RW (2000) Mapping genes that modulate mouse brain development: a quantitative genetic approach. In: Mouse brain development. (Goffinet A, Rakic P, eds), pp 21–49. Berlin: Springer. Williams RW, Strom RC, Goldowitz D (1998a) Natural variation in neuron number in mice is linked to a major quantitative trait locus on Chr 11. J Neurosci 18:138–146. Williams RW, Airey DC, Kulkarni A, Zhou G, Lu L (2001) Genetic dissection of the olfactory bulb of mice: QTLs on chromosomes 4, 6, 11, and 17 modulate bulb size. Behavior Genetics 31: 61–77. |
Neurogenetics at University of Tennessee Health Science Center
| Print Friendly | Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org