Select  Phenotype Database BXDPhenotypeDB BXHPhenotypeDB CXBPhenotypeDB AXB/BXAPhenotypeDB More...       Site search

Publications

Home    Publications

List of Contents Quantitative Neurogenetics & QTL Mapping Genetics of Myopia Control of Neuron Number and Stereology Growth Cones and Dying Axons Retina Development and Visual System Mutants Grant Application U.S. Patent Abstracts Need Help? Help with Publications Help with Nervenet Contact Us

Note to the Reader HTML edition: Copyright © 1998 Robert W. Williams and Karl Herrup Originally published in The Annual Review of Neuroscience 11:423–453 (1988). Last revised Sept 28, 2001. Print Friendly The Control of Neuron Number Robert W. Williams and Karl Herrup Section of Neuroanatomy and Department of Genetics, Yale University School of Medicine, New Haven, Connecticut 06510   Contents Introduction Total neuron number in different species Importance of neuron number Structure of neuron subpopulations Variation in neuron number Importance of rations of neurons Control of neuron proliferation Intrinsic/cell autonomous control of proliferation Single gene effects Lineage-related control of neuron number Extrinsic control Control by cell death Comparative perspective on roles of neuron death Neuron death and neuron ratios Summary and Acknowledgments References   Introduction How an animal senses, perceives, and acts depends on the organization and number of elements that make up its nervous system. Of the several kinds of neural elements, ranging in size from ion channels to cytoarchitectonic divisions, the neuron is the fundamental building block. Understanding processes that control numbers of neurons in the brains of different animals at different stages of development is therefore of great importance. Two approaches can be taken to the problem of neuron number. The first is a cellular and molecular approach that focuses on final effects and final causes that regulate this variable in single species. The second approach has a broader focus on evolutionary, ecological, and bioenergetic reasons for, and consequences of, different strategies used to control the size of neuron populations in different species. Here the aim is to understand the diversity of strategies used to modify neuron number in response to natural selection. This review is divided into three sections. The first section provides an analysis of neuron number in adults of different species. The second and third sections examine the two principal processes that control neuron number during development—neuron production and neuron elimination.   Neuron Number at Maturity Total Neuron Number The total number of neurons in the central nervous system ranges from under 300 for small free-living metazoans such as rotifers and nematodes (e.g., Martini 1912), 30–100 million for the common octopus and small mammals such as shrews and mice (Young 1971, Campbell & Ryzen 1953, Williams 2000), to well over 200 billion for whales and elephants. Estimates for the human brain range between 10 billion and 1 trillion. The imprecision in these estimates is due almost entirely to uncertainty about the number of granule cells in the cerebellum, a problem that can be traced back to a study by Braitenberg & Atwood (1958). More recent work by Lange (1975) makes a reasonably accurate estimate possible: The average human brain (1350 gm) contains about 85 billion neurons. Of these, 12 to 15 billion are telencephalic neurons (Shariff 1953), 70 billion are cerebellar granule cells (Lange 1975), and fewer than 1 billion are brainstem and spinal neurons. [A revision: In a beautiful quantitative analysis of human cortex using the optical disector, Pakkenberg and Gundersen (1997) have shown that the number of neocortical neurons ranges from 15 to 31 billion and averages about 21 billion. Other forebrain structures—primarily the hippocampal region, basal ganglia, and thalamus—are likely to contain an additional 5–8 billion neurons. Total neuron number in humans therefore probably averages 95–100 billion. What is perhaps more remarkable is the normal two-fold difference in neocortical neuron number among healthy adults of normal intelligence.] Behavior complexity is not a function of body size. It follows that an increase in body mass alone does not require a matched increase in numbers of cells. Neurons could simply be larger and could branch more widely (Tower 1954, Purves et al 1986). Nonetheless, larger individuals and larger species generally do have larger brains that do contain more neurons. Even though neurons are larger and packed more loosely in the brains of large species (Holloway 1968, Lange 1975), the increase in brain weight more than offsets the lower density. A 6000-g elephant brain has two to three times as many neurons as does a 1350-g human brain.       In contrast to the paucity and imprecision of data on total neuron number, a great deal is known about the brain weight of vertebrates. This information has been collected in an attempt to provide insight into animal intelligence and evolutionary status (reviewed by Jerison 1985, and Martin & Harvey 1985). That effort has met with little success. As has been repeatedly stressed (Sholl 1948, Mangold-Wirz 1966, Mann et al 1986) and repeatedly ignored, brain mass is a compound variable, and little insight can be gained by reducing brain weight to a simple expression made up of one constant, one variable (usually body weight, surface area, or metabolic rate), and one coefficient (Footnote 1). However, if we can be content with a procrustean generalization, this work does demonstrate that large individuals and large species tend to have large brains. Brain weight is proportional to body weight raised by a power that ranges widely—from 0.1 to 0.8 (Lapicque 1907, Sholl 1948, Stephan 1958, Lande 1979, Ricklefs & Marks 1984). The exponent is less than 1 in all cases; this demonstrates that the increase in brain weight lags behind the increase in body weight. The particular value of the exponent depends in part on the taxonomic level at which comparisons are made. Higher exponents characterize comparisons across orders and classes; lower exponents characterize comparisons at the species level. Exponents between 0.1 and 0.4 are typically derived when comparisons are limited to individuals of the same or closely related species (Wingert 1969, Holloway 1980). However, even within closely related families of species the exponent may vary all the way from 0.2 to 0.6 (Mann et al 1986). This variation is due to differences in ontogenetic, ecological, and evolutionary factors that influence how big a brain a species needs and how big a brain a species can afford.   Importance of Total Neuron Number The number of neurons and their relative abundance in different parts of the brain is a determinant of neural function and, consequently, of behavior. Phyla whose members have larger brains and more neurons respond to environmental change with a greater range and versatility of behavior (Jerison 1985). Orders of mammals with big brains, such as cetaceans and primates, are more clever than those with little brains, such as insectivores and marsupials. However, the correlation breaks down as we narrow the focus and compare allied species and even individuals within species—the exceptions obscure any trend. There is no generally valid equation that relates neuron number to behavioral complexity. For instance, humans of normal intelligence may have brains that weigh only half the average of 1350 gm, and in which there is no evidence for any compensatory increase in neuron density, can have normal intelligence (Hechst 1932, Cobb 1965).       Despite this reservation, there is some experimental evidence of a relation between neuron number and intelligence. Triploid and tetraploid newts have the same brain mass as diploid controls, but their neurons are larger and there are only 50-70% of the normal number (Fankhauser et al 1955, Vernon & Butsch 1957). Although the locomotion of these polyploid newts is indistinguishable from normal, they take two to three times as many trials to learn a maze as do normal newts. Thus, a reduction in neuron number in this case lowers performance markedly. Seasonal oscillations in neuron number in the song nuclei of canaries correlates well with singing ability (Goldman & Nottebohm 1983); this observation lends further support to a notion that many of us have been willing to take on faith. (Footnote 2)       Conversely, in some instances increased neuron number has been shown to result in improved performance. Exposure of immature frogs and rats to excess growth hormone can boost neuron number 20 to 60% according to Zamenhof and colleagues (1941, 1966), and in several instances the hyperplasia or hypertrophy is correlated with improved performance on single-trial avoidance conditioning tasks (Clendinnen & Eayrs 1961, Block & Essman 1965). Similarly, the number of visual cortical neurons excited by one eye has been experimentally increased two-fold in both cats and monkeys, and this increase is associated with smaller receptive fields in visual cortex (Shook et al 1984). Preliminary work supports the idea that such experimental animals are able to resolve smaller differences in the offset between two lines than normal monkeys (M.G. MacAvoy, P. Rakic and C. Bruce, personal communication).   Structure of Neuron Subpopulations The nervous system of all vertebrates and many invertebrates is a mosaic composed of hundreds to thousands of neuron subassemblies. To begin systematic study of the cellular demography of the nervous system we need reliable, objective methods to group neurons together. One way is to group neurons by lineage. The clone of all labeled cells descended from a single precursor cell, whatever the mixture of types, defines the group (Jacobson & Hirose 1978, Weisblat et al 1978, Jacobson & Moody 1984, Sanes et al 1986, Turner & Cepko 1987). The strength of this method in terms of examining relations between lines of neuronal descent, pattern of cell divisions, and the final fate of neurons will be considered in the section on neuron proliferation.       The second, more common way to classify neurons is by shared properties: position, shape, size, axonal projections, electrophysiology, and biochemistry. Neurons of similar type are classed together regardless of whether they are homologous or analogous (Rodieck & Brening 1983, Sternberg & Horvitz 1984). Within a group, neurons may differ enormously in size (Stone 1983), but if the variation is continuous, as is often the case, distinct subpopulations are not recognized. Granule cells of the cerebellar cortex are an example—these cells constitute a huge and nearly homogeneous class that accounts for roughly 7/8 of all neurons in the human brain. However, in the majority of cases, neuron properties vary non-continuously, and populations may thus be broken down repeatedly into a complex hierarchy of sets that share certain features but not others. The retinal ganglion cells of vertebrates have undoubtedly been subjected to such a detailed breakdown to a greater degree than any other cell population (Kolb et al 1981, Stone 1983). These cells are united in being the only neuron population to project out of the retina, but they can be differentiated across other dimensions into as many as 20 to 30 distinct subclasses. If the characteristics of a large enough number of ganglion cells are plotted in a multi-dimensional space, clusters of cells become evident. These clusters provide an objective method to classify neuron phenotype (Rodieck & Brening 1983).       Some neurons do not belong to groups. These neurons are unique and can be recognized individually on the basis of size, cytochemistry, axonal projections, and physiological properties in almost all members of a species. In contrast to the large populations of phenotypically equivalent neurons in vertebrates, the nervous systems of many invertebrates are made up of collections of unique neurons. Essentially all neurons in rotifers (Ware 1971 cited in Ware 1975), nematodes, and leeches are of this type (Goldschmidt 1909, Sulston 1976, Muller et al 1982). The case has even been made that the complex nervous system of grasshoppers, which contain up to 200,000 neurons, may be made up almost entirely of identified neurons and identified neuron clusters (Goodman 1976). In contrast, unique neurons are rare in vertebrates—the Mauthner neuron of fish and amphibians is certainly the best characterized of these (Faber & Korn 1978).       Small clusters of two to six equivalent neurons are also particularly common in the nervous system of invertebrates, for example, the oculomotor neuron clusters in crayfish (Mellon et al 1976) and the heart accessory cells of the leech (Gao & Macagno 1986). While neurons that are part of a cluster are not unique, they are closely allied to identified neurons and are thought to arise by the addition of one to two extra rounds of division at the end of the cell lineage (Goodman 1977, Chalfie et al 1981, Ambros & Horvitz 1984). Identified neurons and neuron clusters will be treated only briefly in this review. When the number of cells of a particular type is one or two, the most interesting questions center around issues of cell commitment and differentiation. In contrast, when populations of neurons are large and variable, the most interesting questions center around the size and composition of the precursor pool, the rate of proliferation, the number of cell divisions, and the patterns of cell death among young neurons. The shift in emphasis is from differentiation to kinetics of proliferation and death.   Variation in Neuron Number Variation in the numbers of neurons in a nucleus or ganglion of a group of animals belonging to the same species is often regarded as an experimental nuisance, and in many cases it is not possible to separate genuine intraspecific diversity from technical artifact (Konigsmark 1970, Williams & Rakic, 1986, 1988 a,b). Unfortunately, this problem masks a fundamental issue. Not only must the absolute number of neurons be regulated during development, but within a population of interbreeding individuals (a deme) there must also be mechanisms that ensure the production and maintenance of adequate variation in numbers of neurons. Without this variation there would be no evolutionary change in either total or relative numbers of neurons (DeBrul 1960, Armstrong 1982). It is important to appreciate that mechanisms that control neuron number also control the range of variation and, ultimately, rates of brain evolution (Mayr 1963). Thus it is not surprising that whenever and wherever it has been looked for with any persistence, natural variation in the numbers of neurons has been found, even in the “invariant” nervous systems of arthropods and annelids (e.g., Lubbock 1858, Hertweck 1931, Goodman 1979, Macagno 1980).       Naturally, there is a balance between the degree of variation and the lowered fitness of individuals at either end of the distribution. Variation will be least in those neuronal systems most exposed to natural selection, and greatest in those systems least exposed to natural selection (Yablokov 1974, Wright 1978). Not only is variation substantial, but the degree of variation is itself highly variable! There can be no blanket statements to the effect that variation is plus or minus 5–10%.       Do small neuron populations show less variation than large populations? If we are willing to settle for the distant view, the answer is, yes. Because each neuron of a small population makes a greater contribution to fitness, it follows that the fewer neurons there are of a given type, the less the tolerable variation in number. Every one of several hundred zebrafish examined by Kimmel and Eaton (1976) had precisely two Mauthner neurons and every one of 50 crayfish examined by Mellon et al (1976) had precisely nine neurons in each ocular motor neuron cluster. In four species of leech studied by Macagno (1979), the variation in neuron number in segmental ganglia was typically under 2%. However, variation in small populations may in some cases be substantial. Kollros and Thiesse (1985) in a careful study of neurons in the mesencepahlic V nucleus of Xenopus frogs found neuron numbers ranged from 185 to 284 at stage 65/66. Left-right differences are also substantial, ranging from 5 to 20% (Kollros & McMurray 1955). Nonetheless, variation in numbers appears to be greatest in particularly large populations of neurons organized in parallel arrays. The range of variation in primate neocortex is greater than +/-50% (van Essen et al 1984, 1986, Williams & Rakic 1986).       In terms of brain evolution it is more important to establish where variation comes from and how it is controlled than the average number of neurons. Is the variation developmental noise, is it experimental noise, or is it a consequence of interactions with the environment? How much of the variation is genetic? And how much of the genetic variation is heritable (additive genetic variance) and how much is not heritable (variance due to epistasis and dominance)? Studies of groups of individuals who have virtually the same genome could in theory provide insight into these issues. Up to the present, however, isogenic individuals have been used almost exclusively to examine the degree to which genetic and epigenetic mechanisms are able to specify neuron phenotype (Macagno et al 1973, White et al 1976, Goodman 1978). The results in some cases reveal remarkably detailed specification. But there have been surprises. For example, some individuals of a single clone of grasshoppers have extra neurons, but others members of the same clone do not (Goodman 1977). Similar variations in meristic traits (traits that can be counted: neurons, scales, hairs, etc.) have been examined closely in isogenic mammals, and here too there is appreciable variation (Newman & Patterson 1911, Storrs & Williams 1968). It is unfortunate that no concerted effort has yet been made to rear isogenic organisms under a wide variety of conditions. Such an experiment could reveal how stable neuron number is in the face of environmental stress (Waddington 1942, Taning 1950, Katz & Lasek 1978).   Importance of Ratios of Neurons It is well accepted that the ratio of different types of neurons in single nuclei and the ratio of neurons in interconnected parts of the nervous system are key determinants of neuronal performance (Wimer et al 1976, Katz & Grenander 1982). However, the limits around which ratios may vary without loss of function are in some cases substantial. For instance, in primates, ratios of neurons in the richly interconnected cytoarchitectonic zones of the occipital lobe (visual areas 17, 18, and 19) vary by more than a factor of two (van Essen et al 1984, 1986, Williams & Rakic 1986), and an equal magnitude of variation is found in ratios of neurons in the peripheral nervous system (Ebbesson 1965). Great variation is also found between ratios of homologous populations of neurons in different species. Here the differences have an easily recognized basis; brains are customized for the body and behavior of each species and consequently ratios of cells will often be radically different. For example, the ratio between granule cells and Purkinje cells rises from less than 200 to 1 in mice to 3000 to 1 in humans (Wetts & Herrup 1982, Lange 1975).       The substantial variations in cell ratios may often be offset by changes in the efficacy and distribution of synapses and the size of axons and dendrites. Consequently, convergence and divergence ratios may be regulated more precisely than are cell ratios. For example, the ratio between preganglionic and postganglionic neurons in the sympathetic nervous system of mammals drops with increasing body size, but the drop is compensated for by an increase in the size and complexity of axons and dendrites (Purves et al 1986).   Brain Metabolism and Neuron Number A variety of studies have shown that a surplus of neurons does not give rise to maladaptive behavior (e.g., Hollyday & Hamburger 1976, Chalupa et al 1984, Ellis & Horvitz 1986); on the contrary, any supernumerary neurons or glial cells can be sequestered or integrated into existing neuronal circuitry and may easily result in more adaptive behaviors. This is as true for roundworms (Ellis & Horvitz 1986) as for rats (Zamenhof 1942). A 20% surplus of neurons in Caenorhabditis elegans caused by a mutation that blocks cell death results in no behavioral deficits in moving, mating, or egg laying (Ellis & Horvitz 1986). What then are the selective pressures that set an upper limit?       Neurons are greedy cells. In resting humans, 18% of circulating oxygen is consumed by brain tissue even though brain makes up only 2% of the body mass (Kety & Schmidt 1948). In infancy the brain is proportionally much larger (Blinkov & Glezer 1968), a situation that is only partially offset by lower metabolic requirements (Kreisman et al 1986). Even during hibernation and estivation, brain metabolism is not reduced appreciably (Meyer & Morrison 1960). Thus neurons represent a high and fixed metabolic expense and the cost of feeding neurons and associated glial cells is undoubtedly one of the principal factors that constrains the total neuron population. (Footnote 3)       The relative cost of neurons depends on an animal's size, its functional metabolic rate (Martin 1981, Armstrong 1983, Armstrong & Bergeron 1985), and the specific metabolic rate of its brain tissue (Krebs 1950). This cost is proportionally highest in small carnivores, birds, and primates, (e.g.,Cebus albifrons ) in which the brain may represent up to 10% of the adult body weight (Spitzka 1903). The nervous system of the 1-mm-long round worm C. elegans takes up an even larger fraction of the body—in the males 381 of 1000 cells are neurons. In terms of body mass devoted to neurons this is the brainiest creature of all. For animals such as these, feeding the brain is a challenge. It is therefore understandable that fecundity in nematodes that must support an extra complement of neurons would be reduced substantially. In fact, brood size in mutants with a 20% increment in neuron number (due to a failure of normal cell death) is 15–30% below normal (Ellis & Horvitz 1986).       The high cost of neurons in small species leads to an interesting prediction: If particular populations of neurons function only seasonally—during mating or while raising young—then it follows that these populations might atrophy or die back when not needed. Such a pattern of loss and replacement has recently been reported in adult canaries—an active bird with a small body and relatively large brain (Goldman & Nottebohm 1983). Here, it is reported that the neuron population in parts of the hyperstriatal complex involved in song production and recognition fluctuates from 41,000 in spring to 25,000 in fall and winter. Similar periodic regression might also be found in other small, highly encephalized homeotherms such as Mustela putorius and Tamias striatrus.       In contrast, large species may be able to afford a superabundance of neurons, even though they may have no pressing need for these cells. The metabolic demands of neurons may represent a minor addition to the total energy consumption of a whale. Alleles that contribute to the production of surplus neurons may be retained in the population because the behavioral and metabolic consequences of doing so are negligible. Although this extra baggage does have a small cost, the capacity to retain more neurons than needed increases the range of variation both in neuron number and in patterns of deployment in different individuals. Maximizing variation increases the evolutionary plasticity of the lineage, an idea analogous to the concept of genetic load—the preservation of alleles in the population that reduce mean fitness but that compensate by providing a reservoir of heritable variation (Mayr 1963). In contrast, an equivalent fractional increase in total neuron number in a small animal will represent a greater increase in the metabolic load and may consequently be strongly selected against (Ricklefs & Marks 1984). Thus, in a mole, canary, or nematode in which the fraction of metabolism devoted to neurons is great, individuals with superfluous neurons will be weeded out quickly.       It follows that the nervous system of small species may be more efficiently designed—that individual neurons may work harder. This is certainly true at a crude level of analysis. At one extreme, the deletion of a single neuron in nematodes lowers fitness to zero by making egg laying impossible (Trent et al 1983), while at the other extreme, the loss of more than 90% of the retinal ganglion cell or Purkinje cell population may result in no detectable behavioral change (Quigley 1981, Wetts & Herrup 1983). However, the analysis should not, and probably cannot, be taken much farther than this—the functional contributions of particular neurons in different parts of the brain is likely to vary widely and depends on much more than just number (Holloway 1968). To take one surprising example, a drop in neuron number in the optic medulla of the "rigidly specified" fruit fly from 40,000 to 20,000 does not cause a clear-cut behavioral effect (Fischbach & Heisenberg 1981).   Control of Neuron Number by Addition In most tissues a deficit of a particular cell type can be corrected by generating new cells, by coaxing cells into the depleted region from surrounding tissues, or by modifing existing cells. As a rule, this is not the case in the nervous system. Precursor cells capable of producing neurons are either few in number or simply do not exist at late stages of development (Miale & Sidman 1961, Rakic 1985). And neurons themselves cannot divide—they are postmitotic cells unable to reenter a cycle of cell division. Consequently, the number of neurons within each part of the nervous system is, with some interesting exceptions, determined at early stages of development, often without the benefit of any exposure to the environment—an odd situation for a organ system designed to deal with the environment. Mature neurons have only limited capabilities to change type or move around. Thus, in contrast to cells in most other tissues, the number, type, and distribution of neurons cannot be regulated about some optimum at maturity. The production and deployment of neurons has to be done right the first time, not an easy job given the extraordinary complexity of the nervous system.       The number of neurons that are generated can be controlled in two ways—by changing numbers of stem cells or by changing numbers of descendants each stem cell produces. Events that alter numbers of stem cells operate early in embryogenesis, but events that change the number of descendants can operate at any time during the expansion of the lineages—the earlier the change, the more dramatic and significant the effects. Changes in precursor number and descendant number can be controlled either by mechanisms that are intrinsic to the population or by mechanisms that are extrinsic. Examples of intrinsic mechanisms are those that affect only cells of a specified lineage or events that are not easily alterable by changing the developmental environment. Examples of extrinsic mechanisms include the influence of heterologous cell interactions, hormones, and environment on the kinetics, commitment, and survival probabilities of stem cells, as well as the recruitment of still uncommitted cells to differentiate into one of several potential subtypes (as during neural crest cell development). Since vertebrates and invertebrates seem to emphasize different areas of this 2 x 2 matrix of possibilities, we have found it convenient to consider the groups separately   Intrinsic Factors In leeches and nematodes, neuron number is under tight control of an inflexible pattern of cell lineage. Shankland and Weisblat (1984) have shown in the leech that if one of a bilateral pair of precursor cells (teloblasts) is eliminated, descendents of the contralateral homologue will occasionally cross the midline. However, this action depletes the donor side to the benefit of the operated side. Up-regulation of cell number either by proliferation or recruitment evidently is not possible, and consequently the question of control of neuron number is rarely raised explicitly in this work. In additional studies the stereotypic patterns of cell lineage were perturbed either by mutation (Horvitz and Sulston, 1980) or by the deletion of cells (Sulston & Horvitz 1977, Kimble & White 1980, Weisblat & Blair 1982). These manipulations have revealed that, while for the great majority of cells lineage constrains their developmental potential to a single fate, for a few other neuroblasts cell-cell interactions specify which of two or three alternate fates—frequently arranged hierarchically—is expressed. In these experiments, the manipulations alter the morphological and numerical fate of the lineage lower on the hierarchy. Thus, again, their is no up-regulation of cell number.       The evidence that cell production in vertebrates is controlled by intrinsic processes is most compelling for non-neuronal tissue. In frog, the mid-blastula transition occurs precisely 12 rounds of division after cleavage. Newport and Kirschner (1982 a,b) have shown that, as in ascidians, it is apparently the ratio of DNA to cytoplasm that is important in triggering the transition. Several other systems also illustrate the point that precursor cells must go through a set number of divisions before the differentiation begins. For example, Quinn and colleagues (1983 a,b, 1984, 1985, 1986) have argued persuasively that precisely four cell divisions are needed between the commitment of a cell to the myogenic lineage and the end of division. Similar evidence has been presented in the case of epidermal stem cells (Potten et al 1982), erythropoietic stem cells (Guesella & Housman 1976), diploid fibroblasts (Angelo & Prothero 1985) and possibly glial progenitor cells (French-Constant & Raff 1986).       In vertebrate nervous system, an elegant analysis of the genesis of the Xenopus lateral line system by Winklbauer and associates (1983) has shown that the number of cells in one lateral line organ is always a multiple of seven times a small but variable integer plus a constant of eight. Their interpretation is that the small number of founder cells of each organ is variable, but once they are committed as founders, a stereotypic series of cell divisions invariably ensues—six asymmetric divisions, each leading to one non-mitotic cell and one new stem cell, followed by one symmetric division that produces two non-mitotic cells. The consequence of this pattern is that neuron number, as well as phenotype, are tightly regulated by the lineage that generate the lateral line.       Evidence for intrinsic mechanisms specifying neuron number during development is implicit in much early work on transplantation of pieces embryonic central nervous system (reviewed in Cooke 1980). However, the methods of analysis are qualitative and only hint at intrinsic mechanisms. As noted by Schoenwolf (1985) there have as yet been no numerical analyses of cell populations that make up the neural plate and tube. It would, for instance, be of considerable theoretical interest to know whether the number of cells in the human neural tube is any greater than the number in the mouse. Single gene effects. Given the relatively large size and complexity of most higher vertebrates and their seemingly non-determinate plan of development, they would seem to be an unlikely place to begin a search for evidence of intrinsic cellular mechanisms controlling rates and fractions of mitotic cells. Yet some of the strongest evidence for intrinsic control of this type come from work on mammals; in particular, from the mouse, and from genetic analyses of the development of this species. A powerful tool in this approach has been the use of genetic mosaics, specifically, the aggregation chimera. This experimental animal is formed by bringing two embryos together at the 8-cell stage of development, coaxing them to form a single embryo and then transplanting the double-blastocyst to a recipient mother where it adjusts in size and finishes gestation.       Several mouse mutations result in the loss of specific sub-sets of neurons. The formation of aggregation chimeras between embryos of these mutant genotypes and wild-type embyros has allowed the demonstration that some events regulating neuron number are caused by the direct action of the mutant gene (reviewed by Mullen & Herrup 1979). The first mutant to be discovered in this category was purkinje cell degeneration (pcd, Mullen, et al 1976). In pcd-pcd mice, 100% of the cerebellar Purkinje cells die beginning at 3 weeks of age. Mullen (1977) analyzed pcd/pcd<->+/+ chimeras and showed that the death of these cells was the autonomous fate of all Purkinje cells of the pcd/pcd genotype. This landmark study revealed that, as in invertebrate systems, the mammalian central nervous system has genes whose proper function is required to produce, or in this case, to retain the proper number of neurons.       A more intriguing, and in some ways more compelling case for the involvement of specific genes in the regulation of neuron number is that of the staggerer (sg) mutant. This autosomal recessive gene, when homozygous, leads to a substantial reduction in the size of the cerebellum and has marked qualitative and quantitative effects on the development of the Purkinje cell population (Sidman 1968, Bradley & Berry 1978, Herrup & Mullen 1979a). In sg/sg<->+/+ chimeras the cerebellum is intermediate in size between mutants and wild-types. Analysis of the chimeras has demonstrated that both the quantitative defects (small cell size, ectopias, regional variation in morphology) and the severe quantitative defect (a 75% reduction in neuron number in homozygous mutants) are only expressed in cells of the sg/sg lineage (Herrup & Mullen 1979, 1981). For example, as shown in Figure 1, if neuron number were reduced non-selectively in chimeras, without regard to genotype, the number of remaining sg/sg genotype neurons would fall somewhere on the curve marked Extrinsic. On the contrary, if only the staggerer lineage were affected by this mutation, then the number of sg/sg-type neuorns in chimeras would fall on the line marked Intrinsic (see Herrup & Mullen 1981). As is clear from the fit of the points (Herrup & Mullen 1981), the data strongly favor an intrinsic over an extrinsic model. The implication of this result is that the mutation at the staggerer gene locus disrupts patterns of cell acquisition or survival within the Purkinje cell lineage in a manner reminiscent of several of the C. elegans lineage mutations.     Figure 1. Two theoretical curves that illustrate the expected number of sg/sg genotype Purkinje cells (PC) in sg/sg by +/+ chimeras, assuming two different modes of gene action (see Herrup & Mullen 1981 for the assumptions and calculations on which these curves are based). The lower line, labeled intrinsic, represents the function expected if the number of sg/sg Purkinje cells is determined by mechanisms that are entirely lineage autonomous. The upper curve shows the function expected if the number of sg/sg Purkinje cells is determined by factors extrinsic to the cells themselves (e.g., hormones, target related cell death, etc.). This extrinsic model predicts that many chimeras should have more sg/sg cells than a nonchimeric sg/sg mouse. The two open circles represent the actual counts of two sg/sg by +/+ animals reported by Herrup & Mullen (1981). The close fit to the intrinsic model suggests that Purkinje cell number in the staggerer is controlled by factors intrinsic to the lineage. 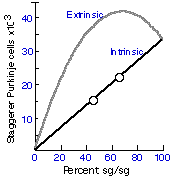The value percent sg/sg is determined by the following formula:      (PC in the chimera – PC in sg/sg) _______________________________    (PC in +/+ – PC in sg/sg)       Lineage-related control of neuron number. These conclusions lead to the notion that specific lineages require specific genes for the regulation of cell number. This raises the question of whether ensembles of lineage-specific factors are involved in the regulation of neuron number. Using lurcher (see above) as a cell marker, Herrup and Wetts (1982c) counted the number of Purkinje cells in a series of lurcher<->wild-type chimeras. Since the cell-autonomous action of the lurcher gene destroys all of the lurcher Purkinje cells, the only cells they could count would have descended from the non-lurcher (wild-type) embryo. They discovered that the counts fell on integral multiples of the value of 10,200 and suggested that this value represented numerical evidence that the population of Purkinje cells consisted of a small number of clones of cells. The number of cells in any one clone is the same and the apparent quantal nature of the Purkinje cells of one genotype in these chimeras reflects the selection of increasing numbers of wild-type cells to found the clones.       Using a mean estimate of 8.5 hours for cell cycle time of neuroblasts (see references in Jacobson 1978), 12.5 embryonic days as the time of the last Purkinje cell division (Miale & Sidman 1961), and assuming the pattern of progenitor cell division is geometric as opposed to asymmetric, it can be estimated that the progenitor cells that give rise to Purkinje cell clones exist as single cells at the earliest stages of mouse nervous system development, approximately the neural plate to neural groove stage. This is precisely the period when prospective surgical analyses suggest that the cells of the neural plate become unalterably established as nervous precursors (Chan & Tam 1986, Beddington 1981, 1983). The retrospective analysis of Wetts and Herrup does not make it possible to determine whether the small pool of precursor cells produce exclusively Purkinje cells and but it is possible to rule out that other cells contribute descendents to the adult population of Purkinje cells.       Extending these studies to the facial nerve nucleus, Herrup et al (1984 ab) were able to show that there was a distinct, clonal organization to this neural structure as well. In the chimeras examined, however, the number of facial nucleus neurons of any one genotype showed no evidence for being an integral multiple of some unit clone size. Instead, Herrup et al. report the existence of “fractional quanta”—the fraction of cells of any one genotype was always divisible by 0.083, or one-twelfth. The best explanation of this finding is that fractional quanta are caused by the elimination of nearly equal numbers of neurons from each of twelve full quanta during a period of cell death (Ashwell & Watson 1983). As a direct consequence, the quantal structure of the population is partially obscured.       Recently, Herrup (1986 a, b) and Herrup and Sunter (1986) have demonstrated the pivotal role cell lineage relationships play in establishing neuron number. Struck by the fact that the size of a Purkinje cell quantum did not change in lurcher chimeras over a wide range of lurcher to wild-type ratios, they examined the clonal relationships of two different inbred strains. The first was the background strain for the lurcher mutant itself, C57BL/6; the second was a different wild-type strain of mouse, AKR/J. In the first instance, the chimeras were mosaics of cells that had identical genotypes at every locus except lurcher. In the second, the cells of the chimeras differed at many loci throughout the genome (Taylor, 1971). Each analysis led to the conclusion that the number of Purkinje cells in these animals occurred in integral multiples of a single value. In the case of C57BL/6, this value was 9,200; in the case of AKR/J, however, this value was 7,850 Purkinje cells. In each analysis, the quantal nature of the counts was maintained over a wide range of mutant/wild-type ratios. This indicates that the size of quanta (i.e., number of Purkinje cells in a clone) is not influenced by the composition of the developmental environment: an AKR/J quantum remains the same size whether it occurs in an animal that is mostly AKR/J or in an animal that is predominantly C57BL/6. Since the latter strain has a different intrinsic clone size, the conclusion can be drawn that the size of a Purkinje cell clone is intrinsic to the lineage. In other words, the number of Purkinje cells that a given progenitor will produce is as much a characteristic of that progenitor as is the morphological type of the cell. This suggests that number as well as form is a property that is ascribed to the early neuroblasts at the beginning of brain development—precisely the same conclusion that was suggested by the analysis of single gene effects.   Extrinsic Factors The evidence cited above suggests that intrinsic, lineage autonomous regulation of neuron number occurs during normal development. This evidence however, does not preclude a role for extrinsic factors. There are, however, few factors that have been identified as either mitogens or mitotic inhibitors that might serve as humoral regulators of neuronal cell division. Nerve growth factor was once thought to be a mitogen of neurons in the peripheral nervous system, but is now known to exert its effects primarily through prevention of cell death and concomitant hypertrophy of the cells (Thoenen & Barde 1980, Thoenen et al 1985). Growth hormone and sex hormones are both candidates for substances with neuronal mitogenic effects. Perhaps the best studied compound of this class is the thyroid hormone, thyroxine.       As early as 1922, Champy showed that factors in the thyroid gland produced a substantial rise in the number of mitotic figures in tadpole retina. Subsequent studies have proven that thyroxine treatment causes an increase in mitotic activity and and an increase in numbers of neurons in retina, telecephalon, and midbrain when given to larval frogs (Zamenhof 1941, Beach & Jacobson 1979, Cline & Constantine-Paton 1986). Zamenhof and colleagues (1942, 1966) have examined the effect of growth hormone in mammals and report a 20% increase in cell density in the cortex of rats treated with growth hormone. An obvious question is whether the hormone is speeding up the rate of cell division or whether additional cells are being recruited in response to growth hormone. Beach and Jacobson (1979) have shown that in the retina of metamorphosing frogs, the effect is due entirely to an increase in the number of dividing cells.       In rodents, administration of thyroxine accelerates the development of the cerebellar cortex and leads to the premature disappearance of the external granule cell layer—site of synthesis of the cerebellar granule cells. Conversely, administration of propylthiouracil, a compound that depletes thyroxine, retards cerebellar development resulting in the persistence of the external granule cell layer, larger cerebellar volumes and increased foliation (Nicholson & Altman, 1972, Lauder et al 1974). These results suggest that by speeding up development, thyroxine can paradoxically decrease total numbers of neuron generated and retained.       Testosterone was initially thought to increase the mitotic activity of the precursors cells that gave rise to ventral hyperstriatum (a song control nucleus) but recent results reveal that the effect is largely attributable to a sex difference in the severity of neuron death (Konishi 1985). Serotonin has also been cited as a potential mitogen. Depleting serotonin in fetal rat prolongs proliferation in those brain regions that ultimately receive serotonergic input (Lauder & Krebs 1976, 1978). 6-hydroxydopamine has been been shown to retard cerebellar growth (Allen et al 1981), suggesting a possible role for noradrenaline uptake systems in regulation of granule cell genesis.       Cell-cell interactions that appear to have a mitogenic effect of neuroblast are also surprisingly rare. There is some evidence that peripheral input is able to modulate the duration or intensity of the proliferation of central neuroblasts (Kollros 1955, Macagno 1979, Chiarodo 1963, Anderson et al 1980). Extirpation of a leg rudiment in blowfly larvae reduces the central neuron population by 30%, an effect that Anderson et al (1980) attribute to a decrease in the production of small local circuit neurons. Similarly, removal of the eye in frogs is reported to reduce mitotic activity in the ventricular zone underlying the tectum (Kollros 1955,). The supposition is that ingrowing axons exert a mitogenic or permissive effect on nearby neuroblasts.       In mammalian cerebellum, several lines of circumstantial evidence suggest that the Purkinje cell exerts a mitogenic influence on the granule cell precursors in the external granule cell layer. These suggestions are based on observations of granule cell kinetics in mutant mice such as reeler (Mariani et al 1977) and staggerer (Landis & Sidman 1978, Mallet et al 1976, Herrup & Mullen 1979, Sonmez & Herrup 1984) and on the regeneration patterns observed after administration of ENU (Das & Pfaffenroth 1977). Finally, the recent work of Raymond and colleagues (1986) and Reh and Tulley (1986) in fish and frog suggests that retinal neurons respond to local cues in making their decision to enter or leave the mitotic cycle.       Certain populations of neurons continue to proliferate at maturity. Arthropod sensory receptor neurons, vertebrate olfactory receptors (Graziadei & Graziadei 1979ab), avian song control neurons (Goldman & Nottebohm 1983) are three examples. There are also small residual populations of neuroblasts in the optic lobes of insects, and in the retina and tectum of fish (Nordlander & Edwards 1968, 1969, Raymond et al 1986, Reh and Tulley 1986). In all these systems, rates of neuron proliferation appear to be controlled via feedback loops. Breaking that loop by sectioning the olfactory nerve, for instance, results in a new burst of neuron proliferation (Graziadei & Graziadei 1979b).       There are a few other less well-substantiated instances of production or recruitment of neurons in adult life. Tritiated thymidine studies of Kaplan (1981) and of Bayer et al (1982) indicate that neurons may be produced, albeit in limited number, in adult rats. Even more difficult to interpret are careful quantitative studies in which counts of presumably postmitotic neuronal populations in rats and mice are observed to increase during postnatal growth. The populations that rise in number include inferior olivary neurons (Delhaye-Bouchaud et al 1985, Caddy & Biscoe, 1979), principal neurons in the dorsal lateral geniculate nucleus (Satorre et al 1986) and Purkinje cells (Caddy & Biscoe 1979, Diglio & Herrup 1982). Most of the authors cited here explain their results as either caused by error of identification in young animals or delayed differentiation of a sub-set of the neurons. Tritiated thymidine studies in most of these systems reveal no apparent genesis of neurons. Nonetheless, the findings are intriguing if only for the cautionary notes they raise about cell counts in developing systems.       Much more is known about the mitogenic effects of neurons and axons on glial cells. DeLong and Sidman (1962) initially showed that removing an eye at birth reduced the number of glial cells in the adult colliculus mainly as a result of decreased rates of glial proliferation. The partial dependence of glial cell proliferation on neurons and humoral mitogens is a particularly active and interesting topic (Raff et al 1978, Perkins et al 1981, Salzer et al 1980, Lemke & Brokes 1983, Nieto-Sampedro 1985).   Control of Neuron Number by Cell Death One of the most counterintuitive and seemingly wasteful processes in brain development is the death of an often large fraction of the initial complement of neurons and glial cells. First noted by Studnicka (1905), Collin (1906), and von Szily (1912) and others in the vertebrate central nervous system, serious attention to this process and the proof that many dying cells are young neurons was delayed until catalytic studies by Glücksmann (1940), Romanes (1946), Hamburger and Levi-Montalcini (1946), Beaudoin 1955, and Hughes (1961). The literature has been particularly well reviewed (Källén 1965, Hughes 1968; Prestige 1970, Cowan 1973, Silver 1978, Jacobson 1978, Cunningham 1982, Berg 1982, Beaulaton & Lockshin 1983, Hamburger & Oppenheim 1983, Horvitz et al 1982, Truman 1984, Oppenheim 1987).   Variation Neuron death is by no means universal throughout the animal kingdom. The process in unknown in Aplysia californica (Jacob 1984), and is also rare or unknown in elasmobranchs (sharks and rays), teleosts, or reptiles (but see Fox & Richardson 1982). There is no evidence of motor neuron loss in zebrafish, dogfish, or stingray (reviewed in Mos & Williamson 1986). With the important exception of birds, mammals, and nematodes, it appears that the elimination of neurons is most pronounced in species that undergo metamorphosis, and is least pronounced in vertebrates and invertebrates that do not metamorphose and that grow throughout life.       The incidence of death among different populations of neurons also shows great variation in single species—there is no meaningful average incidence. Some populations are eliminated completely (Studnicka 1905, Hughes 1957 Munk 1966, Stewart et al 1987), while other populations live happily ever after (e.g. Armstrong & Clarke 1979, Mos & Williamson 1986). Even within groups of neurons the distribution of dying cells is uneven. For instance in the mammalian neocortex degeneration is restricted almost entirely to the upper two layers (Finlay & Slattery 1983; Williams et al., 1987), and in spinal cord and dorsal root ganglia, degeneration is most severe in segments that do not innervate the limbs (Levi-Montalcini 1950, Hamburger 1975). The magnitude of neuron death within homologous populations in different species is also remarkably variable. For instance, 80% of retinal ganglion cells die in cat (Williams et al 1986); 60–70% in rat and mouse (Crespo et al 1985; Strom and Williams, 1998), rhesus monkey, and human (Rakic & Riley 1983, Provis et al 1985); 40% in chicken (Rager 1980), and none whatsoever in fish or amphibia (Wilson 1971, Easter et al 1981).       Sex-specific variation in patterns of neuron death have also recently been demonstrated in warm-blooded vertebrates (Konishi 1985, Nordeen et al 1985). In rats, for instance, the the pool of motor neurons innervating penis muscles contains 160–200 neurons in males whereas a homologous pool in females contains only 35#150;60 small neurons (Breedlove & Arnold 1980, Nordeen et al 1985). The 3- to 4-fold difference is brought about by a more severe loss in females during the first 10 postnatal days (Nordeen et al 1985). Compare this strategy with that used by annelids. In leech the two segmental ganglia associated with the sex organs contain twice the baseline number of neurons found in the other ganglia. The abrupt regional difference is not brought about by modulation of the severity of cell loss across the entire series of segments (this really would be wasteful). Instead the neurons are simply added selectively to the sex ganglia late in development (Ogawa 1939, Stewart et al 1986).   Comparative Perspective on Roles of Neuron Death In nematodes neuron death is not contingent on the status of other cells. Death is an inflexible autonomous fate that serves to eliminate neurons that are apparently unwanted byproducts of patterns of cell lineage. In C. elegans one common mechanism, involving the action of at least four ced gene products, catalyzes the death of most cells—neurons included. Mutations of the genes ced-3 and ced-4 prevent degeneration and death entirely (Hedgecock et al 1983, Ellis & Horvitz 1986). The most probable reason why neurons die in nematodes is not to remove potentially detrimental neurons, but to rid the organisms of unneeded, metabolically demanding cells. In this animal, neuron elimination appears to be strictly a means to regulate number, not to regulate ratios of cells or to improve neuronal performance. However, in many, if not most other phyla, the process of cell elimination in any one population of neurons is regulated by several different kinds of interactions, each designed to optimize cell number or cell performance along a different parameter. Here, neuron death is just the final common pathway of disparate processes having disparate causes. The relative contributions of these processes will differ from animal to animal, from neuron population to neuron population.       For instance, even in insects in which neuron death often appears to be under the same rigid genomic control noted in nematode (Whitington et al 1982), there are several interesting exceptions in which the loss is absolutely contingent on cell environment and even animal behavior (Truman 1983). For instance, the severe necrosis in the optic lobes of the eyeless fruit fly mutant, so, is triggered by the degeneration of the eye imaginal disc cells (Hofbauer & Campos-Ortega 1976, Fischbach & Technau 1984). This is an important advance—neuron death in holometabolous insects is no longer an inflexible attribute of certain young neurons.       In chordates neuron loss appears to be catalyzed in large part by the hormonal, vascular, and cellular environments in which neurons and their processes are situated. Thyroxine for example catalyzes the radical transformations in body architecture in amphibians that are associated with a rapid and focal loss of select neuron populations (Hughes 1961, Torrence 1983). All Rohan-Beard neurons are lost in frogs over a short period at the climax of metamorphosis (Hughes 1957). In warm-blooded vertebrates, naturally occurring neuron death is often very substantial and is in most cases at least partially explicable in terms of the size and status of the target (see reviews cited above), the density of synaptic input onto dendrites and cell bodies (Linden & Perry 1982, Okada & Oppenheim 1984), nutritional status (Dobbing & Smart 1974), and hormone levels (Nordeen et al 1985). In some cases, neuron death rids the brain of neurons that fail to make correct connections (e.g., Clarke & Cowan 1976, McLoon 1981, Jacobs et al. 1984, O'Leary et al 1986). More to the point of this chapter, neuron death appears to have a major role is the final adjustments of ratios of interconnected neurons.   Neuron Death and Neuron Ratios The rate and duration of neuron production in distant populations that are ultimately interconnected may not be well matched. This will produce quantitative imbalances.4  Cell elimination provides a way to adjust ratios of cells after a link between interconnected populations by axons or dendrites has been established. The larger the nervous system and the more disjoint the production of interconnected cell populations (e.g., motor neurons and muscle fibers, pre- and post-ganglion sympathetic neurons, receptor neurons and central target cells), the more important secondary fine-tuning will be. For example, motor neurons in vertebrates are lost shortly after their axons have reached target musculature. If the target is removed early enough in development (before or during the period of cell death) then the severity of neuron loss is increased. Cell death can wipe out the entire population if the target is removed early enough in development (e.g. Hughes & Tschumi 1954, Lancer & Fallon 1984). Complementary studies in which the the size and number of target cells is increased have been carried out in several systems (e.g., Hamburger 1939, Hollyday and Hamburger 1976, Pilar et al 1980, Boydston and Sohal 1979, Narayanan and Narayanan 1978, Lamb 1979, Chalupa et al. 1984, Maheras & Pollack 1985). In all cases, an increase in number of targets cells causes an appreciable increase in the percentage of surviving neurons, but the increase is never as great as would be required to maintain a normal ratios between interconnected cells. Thus, neuron elimination even in these systems is not regulated entirely by extrinsic factors. Some fraction of the loss is evidently intrinsic and thus cannot be regulated during ontogeny to bring about the most adaptive ratio between cells. However, the long term selective pressures on a species may result in rather rapid change in the importance of intrinsic control. As pointed out by Prestige (1970), the relative weight of intrinsic and extrinsic control varies substantially between vertebrate classes. For example, the loss of thoracic motor neurons in the anuran spinal cord is heavily dependent on the status of the periphery, whereas the loss of the same population of neurons in chick and mouse appears to be largely under intrinsic control. This specific difference may be related to the fact that anurans metamorphose, whereas birds and mammals develop directly.       We remarked above that there was only limited direct evidence that either the number of the neurons in any one nucleus or the ratio in two interconnected populations is important. The suggestion was that evolution, as the final judge, can detect differences that neurobiologists do not detect. The remarkable precision of the numerical regulation that is apparent during the development of some neuron populations strengthens this proposition. For instance, there is now evidence that ratios of interconnected cells are regulated precisely by naturally occurring cell death. Tanaka and Landmesser (1986 a,b) examined spinal motor neurons in chick, quail, and chick<->quail chimeras. The ratios of neurons and primary myotubes for each condition was constant. Lanser and Fallon (1987) have extended this work and shown that the number of surviving motor neurons in wingless mutant chicks (a mutation with variable penetrance) is a linear function of the mass of the limb musculature.       A direct correlation between neuron number and target size has also been demonstrated in the central nervous system. Wetts and Herrup (1983) observed a linear relation between Purkinje cell and granule cell numbers in several wild-type strains of mouse, and experimental studies of staggerer<->wild-type mice chimeras provided further proof that ratios are regulated quite precisely. Staggerer granule cells are not intrinsically programmed to die (Herrup 1983). Thus in a staggerer chimera more granule cells are produced than can be supported by the healthy, wild-type Purkinje cells. This imbalance is corrected by an increased incidence of cell death (Sonmez & Herrup 1984), and the result is a linear relationship between granule cell and Purkinje cell numbers (Herrup & Sunter 1987). Achieving an optimal match in numbers of interconnected cells is undoubtedly one important role of neuron elimination.       Neuron loss can be interpreted as contributing to an individual's fitness either by improving the efficiency of information processing or the efficiency of metabolism. At a higher level of analysis the combination of overproduction and loss of neurons may also buffer and conserve heritable variation and thereby increase the evolutionary plasticity of a species (Katz & Lasek 1978, Williams et al 1986, Finlay et al 1987; [Williams et al., 1994]). However, experimental demonstrations that the combination of neuron overproduction and neuron elimination makes a particular contribution to fitness of individuals and species will continue to be hard to obtain. We will almost certainly understand the cell biology of neuron elimination before we understand the underlying cause and utility.   Summary In comparing strategies used to control neuron number, we find it useful to view nervous system development as occurring in three phases. The phases overlap—each is a process, not an event. The first phase is the development of a genetic nervous system. This is a nervous system of simple genetic intention; not a blueprint or pile of bricks. Its characteristics are abstract: how many neurons is this stem cell destined to produce, which cells are programmed to die, how much target does this cell need to survive. At the level of the individual, the genetic nervous system is essentially fixed, but over generations it is fluid. As this genetic intent interacts within a world of cells, a real brain to appears. A new set of rules only tacitly present in the genome is expressed—the embryonic nervous system emerges. The interaction of its parts defines the shape and size of the nervous system. Neuron numbers are adjusted interactively by changes in proliferative potential and the severity of cell death. Cell fates are established in part through interactions with other cells and with hormones. Glial cell numbers are adjusted to match the neuron populations. This phase of brain development is what the embryologist sees under the microscope. The final phase of development begins when the brain starts to function and the animal starts to deal with its world. Small changes in neuron number may occur.during this period, but the changes are generally of minor functional importance. At this point, the smaller elements of neuronal organization are refined in shape, number, and distribution. Axons are lost or rearranged; dendrites grow, branch, and retract; synapses are fine-tuned; and finally, receptors densities and transmitter titres are adjusted. Some of these interactions and numerical adjustments continue until the animal dies. ACKNOWLEDGMENT.   We thank Kathryn Graehl for editorial help. Supported in part by grants NS 20591, NS18381, and the March of Dimes 1-763.   References Allen, C. Sievers, J., Berry, M., Jenner, S. 1981. Experimental studies on cerebellar foliation. II. A morphometric analysis of cerebellar fissuration defects and growth retardation after neonatal treatment with 6-OHDA in the rat. J. Comp. Neurol. 203: 771–83 Ambros, V., Horvitz, H.R. 1984 Heterochronic mutants of the nematode Caenorhabditis elegans. Science 226: 409–16 Anderson, H., Edwards, J.S., Palka, J. 1980. Developmental neurobiology of invertebrates. Ann. Rev. Neurosci. 3: 97–139 Angelo, J.C., Prothero, J.W. 1985. Clonal attenuation in chick embryo fibroblasts. Experimental data, a model and computer simulations. Cell Tissue Kinet. 18: 27–43 Armstrong, E. 1982. Mosaic evolution in the primate brain: Differences and similarities in the hominoid thalamus. In Primate Brain Evolution. Methods and Concepts. ed. E. Armstrong, D. Falk, pp. 131–61. New York: Plenum Press Armstrong, E. 1983. Relative brain size and metabolism in mammals. Science 220: 1302–4 Armstrong, E., Bergeron, R. 1985. Relative brain size and metabolism in birds. Brain Behav. Evol. 26: 141–53 Armstrong, R.C., Clarke, P.G.H. 1979. Neuronal death and the development of the pontine nuclei and inferior olive in the chick. Neuroscience 4: 1635–47 Ashwell, K.W. and Watson, C .R.R. (1983). The development of facial motoneurones in the mouse—Neuronal death and the innervation of the facial muscles. J. Embryol. Exp. Morphol. 77: 117–41 Beach, D.H., Jacobson, M. 1979. Influence of thyroxine on cell proliferation in the retina of the clawed frog at different ages. J. Comp. Neurol. 183: 615–24 Beaudoin, A.R. 1955. The development of lateral motor column cells in the lumbo–sacral cord in Rana pipiens, I. Normal development and development following unilateral limb ablation. Anat. Rec. 121: 81–95 Beaulaton, J., Lockshin, R.A. 1982. The relation of programmed cell death to development and reproduction: Comparative studies and an attempt at classification. Int. Rev. Cytol. 79: 215–35 Beddington, R.S.P. 1981. An autoradioagraphic analysis of the potency of embryonic ectoderm in 8th day postimplantation mouse embryos. J. Embryol. Exp. Morph. 69: 265–85 Beddington, R.S.P. 1983. Histogenic and neoplastic potential of different regions of mouse embryonic egg cylinder. J. Embryol. Exp. Morph. 75: 189–204 Berg, D.K. (1982) Cell death in neuronal development. Regulation by trophic factors. In Neuronal Development, ed. N.C. Spitzer, pp. 297–331. New York: Plenum Blinkov, S.M., Glezer, I.I. 1968. The Human Brain in Figures and Tables: A Quantitative Handbook. New York: Basic Books, Inc. Plenum Press Block, J.B., Essman, W.B. 1965. Growth hormone administration during pregnancy: A behavioural difference in offspring rats. Nature 205:1136–37 Boydston, W.R., Sohal, G.S. 1979. Grafting of additional periphery reduces embryonic loss of neurons. Brain Res. 178: 403–10 Bradely, P., Berry, M. 1978 Purkinje cell dendritic tree in mutant mouse cerebellum. A quantitative Golgi study of weaver and staggerer mice. Brain Res. 142: 135–41. Braitenberg, V., Atwood, R.P. 1958. Morphological observations on the cerebellar cortex. J. Comp. Neurol. 109: 1–33. Breedlove, S.M., Arnold, A.P. 1980. Hormone accumulation in a sexually dimorphic motor nucleus of the rat spinal cord. Science 210: 564–566. Bullock, T.H., Horridge, G.A. 1965 Structure and Function in the Nervous System of Invertebrates. San Francisco: Freeman. Bush G.L., Case S.M., Wilson, A.C., and Patton J.L 1977. Rapid speciation and chromosomal evolution in mammals. Proc. Natl. Acad. Sci. USA 74: 3942–46 Caddy, K.W.T.& Biscoe,T.J. 1979. Structural and quantitative studies on the normal C3H and Lurcher mutant mouse. Phil T. Roy. Soc. Lond Ser. B 287: 167–201 Campbell, B., Ryzen, M. 1953. The nuclear anatomy of the diencephalon of Sorex cinereus. J. Comp. Neurol. 99: 1–22 Chalfie, M., Horvitz, H.R., Sulston, J.E. 1981. Mutations that lead to reiterations in the cell lineage of C. elegans. Cell 24: 59–81 Chalupa, L.M., Williams, R. W., Henderson, Z. 1984. Binocular interaction in the fetal cat regulates the size of the ganglion cell population. Neuroscience 12: 1139–46 Champy, C. 1922. L'action de l'extrait thyroidien sur la multiplication cellulaire. Caracter electif de cette action. Arch. Morphol. Gen. Exper. 4: 1–58 Chan, W.Y., Tam, P.P.L. 1986. The histogenetic potential of neural plate cells of early somite–stage mouse embryos. J. Embryol. Exp. Morphol. 96: 183–93 Chiarodo, A.T. 1963. The effects of mesothoracic leg disc extirpation on the postembryonic development of the nervous system of the blowfly Sarcophaga bullata. J. Exp. Zool. 153: 263–77 Clarke, P.G.H., Cowan W.M. 1976. The development of the isthmo–optic tract in the chick, with special reference to the occurrence and correction of developmental errors in the location and connection of isthmo–optic neurons. J. Comp. Neurol. 167:143–64 Clendinnen, B.G., Eayrs, J.T. 1961. The anatomical and physiological effects of prenatally administered somatotrophin on cerebral development. J. Endocrinol. 22:183–93 Cline, H.T., Constantine–Paton, M. 1986. Thyroxine effects on the development of the retinotectal projection. Soc. Neurosci. Abs. 12:437 Cobb, S. 1965. Brain size. Arch. Neurol. 12:555–61 Collin, R. 1906–1907. Recherches cytologiques sur le developpement de la cellule nerveus. Nevraxe 8:181–303 Cooke, J. 1980. Early organization of the central nervous system: Form and pattern. Curr. Top. Devel. Biol. 15:373–407 Cowan, W.M. 1973. Neuronal death as a regulative mechanism in the control of cell number in the nervous system. In Development and Aging in the Nervous System, ed. M. Rockstein, pp. 19–41. New York: Academic Press Crespo, D., O'Leary, D.D.M., Cowan, W.M.1985. Changes in the number of optic nerve fibers during late prenatal and postnatal development in the albino rat. Dev. Brain Res. 19:129–34 Cunningham, T.J. 1982. Naturally occurring neuron death and its regulation by developing neural pathways. Internat. Rev. Cytol. 74: 163–86. Das, G.D. and Pfaffenroth, M.J. 1977. Experimental studies on the postnatal development of the brain. III. Cerebellar development following localized administration of ENU. Neuropath. Appl. Neurobiol. 3:191–212 DeBrul, L. 1960. Structural evidence in the brain for a theory of the evolution of behavior. Perspect. Biol. Med. 4:40–57. Delhaye–Bouchaud, N., Geoffroy, B., Mariani, J. 1985. Neuronal death and synapse elimination in the olivocerebellar system. I. Cell counts in the inferior olive of developing rats. J. Comp. Neurol. 232:299–308 DeLong, G.R., Sidman, R.L. 1962 Effects of eye removal at birth on histogenesis of the mouse superior colliculus: An autoradiographic analysis with tritiated thymidine. J. Comp. Neurol. 118:205–23 Diglio, T., Herrup, K. 1982. A significant fraction of the adult number of mature cerebellar Purkinje cells first appears between postnatal days 16 and 30 in the mouse. Soc. Neurosci. Abst. 8:636 Dobbing, J., Smart J.L. 1974. Vulnerability of developing brain and behaviour. Brit. Med Bull. 30:164–68. Easter, S.S., Jr., Rusoff, A.C., Kish, P.E. 1981. The growth and organization of the optic nerve and tract in juvenile and adult goldfish. J. Neurosci. 1:793–811. Ebbesson, S.O.E. 1965. Quantitative studies of superior cervical sympathetic ganglia in a variety of primates including man. I. The ratio of preganglionic fibers to ganglionic neurons. J. Morph. 124:117–32 Eisenberg, J.F. 1981. The Mammalian Radiations. An Analysis of Trends in Evolution, Adaptation, and Behavior. Chicago: The University of Chicago Press Eisenberg, J.F., Wilson D.E. 1982. Relative brain size and feeding strategies in the Chiroptera. Evolution 32: 740–51 Ellis, H.M., Horvitz, H.R. 1986. Genetic control of programmed cell death in the nematode C. elegans. Cell 44:817–29 Faber, D.S., Korn, H., eds. 1978. Neurobiology of the Mauthner Cells. New York: Raven Press Fankhauser, G., Vernon, J.A., Frank, W.H., Slack, W.V. 1955. Effect of size and number of brain cells on learning in larvae of the salamander, Triturus viridescens. Science. 122:692–93 Finlay, B.L., Slattery, M. 1983. Local differences in the amount of early cell death in neocortex predict adult local specializations. Science 219:1349–51 Finlay, B.L., Wikler, K.C., Sengelaub, D.R. 1987. Regressive events in brain development and scenarios for vertebrate brain evolution. Brain Behav. Evol. 30:102–17 Fischbach, K.F., Heisenberg, M. 1981. Structural brain mutant of Drosophila melanogaster with reduced cell numbers in the medulla cortex and with normal optomotor yaw response. Proc. Natl. Acad. Sci. USA 78:1105–9 Fischbach, K.F., Technau, G. 1984. Cell degeneration in the developing optic lobes of the sine oculis and small–optic–lobes mutants of Drosophila melanogaster. Devel. Biol. 104:219–39 Fox, G.Q., Richardson, G.P. 1982. The developmental morphology of Torpedo marmorata: Electric lobe–electromotoneuron proliferation and cell death. J. Comp. Neurol. 207:183–90 Gao, W–Q., Macagno, E. R. 1986. Extension and retraction of axonal projections by existence of neighboring homologues. I. The HA cells. J. Neurobiol. 18: 43–59 Glucksmann, A. 1940. Development and differentiation of the tadpole eye. Brit. J. Ophthal. 24:153–78 Glucksmann, A. 1951. Cell deaths in normal vertebrate ontogeny. Biol. Rev. 26:59–86 Goldschmidt, R. (1909) Das Nervensystem von Ascaris lumbridoides und megalodephala. II. Z. Wiss. Zool. 92:306–57 Goldman, S.A., Nottebohm F. 1983. Neuronal production, migration, and differentiation in a vocal control nucleus of the adult canary brain. Proc. Natl. Acad. Sci. USA 80:2390–94 Goodman, C. 1976. Constancy and uniqueness in a large population of small interneurons. Science 193:502–4 Goodman, C.S. 1977. Neuron duplications and deletions in locust clones and clutches. Science 197:1384–86 Goodman, C.S. 1978. Isogenic grasshoppers: Genetic variability in the morphology of identified neurons. J. Comp. Neurol. 182:681–706 Goodman, C.S. 1979 Isogenic grasshoppers: Genetic variability and development of identified neurons. In Neurogenetics: Genetic Approaches to the Nervous System, ed. X.O. Breakfiled, pp. 101–51. New York: Elsevier–North Holland Gould S.J. 1977. Ontogeny and Phylogeny. The Belknap Press of Harvard University Press, Cambridge, Mass Graziadei, P.P.C., Monti Graziadei, G.A. 1979 a. Neurogenesis and neuron regeneration in the olfactory system of mammals. I. Morphological aspects of differentiation and structural organization of the olfactory sensory neurons. J. Neurocytol. 8:1–18 Graziadei, P.P.C., Monti Graziadei, G.A. 1979b. Neurogenesis and neuron regeneration in the olfactory system of mammals. II. Degeneration and reconstitution of the olfactory sensory neurons after axotomy. J. Neurocytol. 8:197–213 Guesella, J., Geller, R., Clarke, B., Weeks, V., Housman, D. 1976. Commitment to erythroid differentiation by Friend erythroleukemia cells. A stochastic analysis. Cell 9:221–29 Hamburger, V. 1939. Motor and sensory hyper–plasia following limbbud transplantations in chick embryos. Physiol. Zool. 12:268–284 Hamburger, V. 1975. Cell death in the development of the lateral motor column of the chick embryo. J. Comp. Neurol. 160:535–46 Hamburger, V., and Levi–Montalcini, R. 1949. Proliferation, differentiation and degeneration in the spinal ganglia of the chick embryo under normal and experimental conditions. J. Exp. Zool. 111: 457–501 Hamburger, V., Oppenheim, R. W. 1982. Naturally occurring neuronal death in vertebrates. Neurosci. Comm.1: 39–55 Hechst, B. 1932. Uber einen Fall von Mikroencephalie ohne geistigen Defekt. Arch. Psychiat. u. Nervenk. 97:64–76 Hedgecock, E., Sulston, J.E., Thompson, N. 1983. Mutations affecting programmed cell deaths in the nematode Caenorhabditis elegans. Science 220:1277–80 Herrup, K. 1986. Cell lineage relationships in the development of the mammalian CNS: Role of cell lineage in control of cerebellar Purkinje cell number. Devel. Biol. 115:148–54 Herrup, K. 1983. Role of staggerer gene in determining cell number in cerebellar cortex. I. Granule cell death is an indirect consequence of staggerer gene action. Devel. Brain Res. 11:267–74 Herrup, K., 1987 Roles of cell lineage in the developing mammalian brain. Curr. Top. Devel. Biol 21: 65–97 Herrup, K., Mullen, R.J. 1979. Staggerer chimeras: Intrinsic nature of Purkinje cell defects and implications for normal cerebellar development. Brain Res. 178:443–57 Herrup, K., Mullen, R.J. 1981. Role of the staggerer gene in determining Purkinje cell number in the cerebellar cortex of mouse chimeras. Dev. Brain Res. 1:475–85 Herrup, K., Wetts, R., Diglio, T.J. 1984a. Cell lineage relationships in the development of the mammalian CNS. II. Bilateral independence of CNS clones. J. Neurogenet. 1:275–88 Herrup, K., Letsou, A., Diglio, T.J. 1984b. Cell lineage relationships in the development of the mammalian CNS: The facial nerve nucleus. Devel. Biol. 103:329–36 Herrup, K., Sunter, K. 1986 Cell lineage dependent and independent control of Purkinje cell number in the mammalian CNS: Further quantitative studies of Lurcher chimeric mice. Devel. Biol 117: 417–27 Herrup, K , Sunter, K. 1987. Numerical matching during cerebellar development: Quantitative analysis of granule cell death in staggerer mouse chimeras. J. Neurosci. 7:829–836 Hertweck, H. 1931. Anatomie und Variabilitat des Nervensystems und der Sinnesorgane von Drosophila melanogaster (Meigen). Z. Wiss. Zool. 139:559–663 Hinds, J.W., Hinds P.L. 1978. Early development of amacrine cells in the mouse retina: An electron microscopic, serial section analysis. J. Comp. Neurol. 179: 277–300 Hofbauer, A., Campos–Ortega, J.A. 1976. Cell clones and pattern formation: Genetic eye mosaics in Drosophila melanogaster. Wilhelm Roux Arch. Devel. Biol. 179:275–89 Holloway, R.L. 1968. The evolution of the primate brain: Some aspects of quantitative relations. Brain Res. 7:121–72 Holloway, R.L. 1980. Within–species brain–body weight variability: A reexamination of the Danish data and other primate species. Am. J. Phys. Anthropol. 53:109–21 Hollyday, M., Hamburger, V. 1976. Reduction of the naturally occurring motor neuron loss by enlargement of the periphery. J. Comp. Neurol. 170:311–20 Horvitz, H.R., Ellis, H.M., Sternberg P.W. 1982. Programmed cell death in nematode development. Neurosci. Comment. 1:56–65 Hughes, A.F. 1957. The development of the primary sensory system in Xenopus laevis (Daudin). J. Anat. 91:323–38 Hughes, A.F. 1961. Cell degeneration in the larval ventral horn of Xenopus laevis. J. Embryol. Exp. Morph. 9:269–84 Hughes, A. 1968. Aspects of Neural Ontogeny. New York, Academic Press Hughes, A., Tschumi, P.A. 1958. The factors controlling the development of the dorsal root ganglia and ventral horn in Xenopus laevis (Daud.) J. Anat. 92:498–527 Jacob, M.H. (1984) Neurogenesis in Aplysia californica resembles nervous system formation in vertebrates. J. Neurosci. 4:1225–39 Jacobs, D.S., Perry, V.H., Hawken, M.J. (1984) The postnatal reduction of the uncrossed projection from the nasal retina in the cat. J. Neurosci. 4: 2425–33 Jacobson, M. 1978. Developmental Neurobiology. 2nd ed., New York: Plenum Press Jacobson, M. 1985. Clonal analysis and cell lineages of the vertebrate central nervous system. Ann. Rev. Neurosci. 8:71–102 Jacobson, M., Hirose, G. 1978. Origin of the retina from both sides of the embryonic brain: A contribution to the problem of crossing at the optic chiasma. Science 202:637–39 Jacobson, M., Moody, S.A. 1984. Quantitative lineage analysis of the frog's nervous system. I. Lineages of Rohon–Beard neurons and primary motoneurons. J. Neurosci. 4:1361–69 Jerison, H.J. 1955. Quantitative analysis of evolution of the brain in mammals. Science 133:1012–14 Jerison, H. J. 1973. Evolution of the Brain and Intelligence. New York. Academic Press Jerison, H.J. 1985. Animal intelligence as encephalization. Phil. Trans. R. Soc. Lond.Ser. B. 308:21–35 Källén, B. 1955 Cell degeneration during normal ontogenesis of the rabbit brain. J. Anat. 89:153–62 Källén, B. 1965. Degeneration and regeneration in the vertebrate central nervous system during embryogenesis. Prog. Brain Res. 14:77–96 Kaplan, M.S. 1981. Neurogenesis in the 3–month–old rat visual cortex. J. Comp. Neurol. 195:323–38 Katz, M.J., Lasek, R.J. 1978. Evolution of the nervous system: Role of ontogenetic mechanisms in the evolution of matching populations. Proc. Natl. Acad. Sci. USA 75: 1349–52 Katz, M.J., Grenander, U. 1982. Developmental matching and the numerical matching hypothesis for neuronal cell death. J. Theor. Biol. 98:501–17 Kety, S.S., Schmidt, C.F. 1948. The effects of altered arterial tensions of carbon dioxide and oxygen on cerebral blood flow and cerebral oxygen consumption of normal young men. J. Clin. Invest. 27:484–492 Kimmel, C.B., Eaton, R.C. 1976. Development of the Mauthner cell. IN Simpler Networks and Behavior. ed. J.C. Fentress, pp. 186–202. Sunderland, Mass, Sinauer Kolb, H., Nelson, R., Mariani, A. 1981. Amacrine cells, bipolar cells and ganglion cells of the cat retina: A Golgi study. Vision Res. 21:1081–1114 Kollros, J.J. 1953 The development of the optic lobes in the frog. I. The effects of unilateral enucleation in embyronic stages. J. Exp. Zool 123: 153–87 Kollros, J.J., McMurray, V.M. 1955. The mesencephalic V nucleus in anurans. J. Comp. Neurol. 102:47–61 Kollros, J.J. 1982. Peripheral control of midbrain mitotic activity in the frog. J. Comp. Neurol. 205:171–178 Kollros, J.J., Thiesse M.L. 1985. Growth and death of cells of the mesencephalic fifth nucleus in Xenopus laevis larvae. J. Comp. Neurol. 233:481–489 Konigsmark, B.W. 1970. The counting of neurons. In Contemporary Research Methods in Neuroanatomy, eds. W.J.H. Nauta and S.O. Ebbesson, pp. 315–40. New York: Springer Verlag Konishi, M. 1985. Birdsong: From behavior to neuron. Ann. Rev. Neurosci. 8:125–70 Krebs, H.A. 1950 Body size and tissue respiration. Biochim. Biophys. Acta 4:249–269 Kreisman, N.R., J. E. Olson, D.S. Horne, Holtzman, D. 1986. Developmental increases in oxygen delivery and extraction in immature rat cerebral cortex. Neurosci. Abs. 12:451. Lamb, A.H. 1979. Evidence that some developing limb motoneurons die for reasons other than peripheral competition. Dev. Biol. 71:8–21 Lande, R. 1979. Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 33:402–416 Landis, D.M.D. and Sidman, R.L. 1978. Electron microscopic analysis of postnatal histogenesis in the cerebellar cortex of staggerer mutant mice. J. Comp. Neurol. 179:831–863. Lange, W. 1975 Cell number and cell density in the cerebellar cortex of man and other mammals. Cell Tiss. Res. 157: 115–24 Lanser, M.E., Fallon, J.F.1984. Development of the lateral motor column in the limbless mutant chick embryo. J. Neurosci. 4:2043–50 Lanser, M.E., Fallon, J.F. 1987 Development of the branchial lateral notor column in the Wingless mutatnt chick embryo: Motoneuron survival under varuying degrees of peripheral load. J. Comp. Neuro. 261: 423–34 Lapicque, L. 1907. Le poids encephalique en fonction du poids corporel entre individus d'une meme espece. Bull. Mem. Soc. Anthropol. Paris. 8:313–45 Lauder, J.M., Altman, J., Krebs, H. 1974. Some mechanisms of cerebellar foliation: effects of early hypo– and hyperthyroidism. Brain Res. 76:33–40 Lauder, J.M., Krebs, H. 1976. Effects of p–chlorophenylalanine on time of neuronal origin during embryogenesis in the rat. Brain Res. 107:638–44 Lauder, J.M., Krebs, H. 1978. Serotonin as a differentiation signal in early neurogenesis. Dev. Neurosci. 1:15–30 Lemke, G.E., Brokes, J.P. 1983. Identification and purification of glial growth factor. J. Neurosci. 4:75–83 Levi–Montalcini, R. 1950. The origin and development of the visceral system in the spinal cord of the chick embryo. J. Morphol. 86:253–83 Linden, R., Perry, V.H. 1982. Ganglion cell death within the developing retina: A regulatory role for retinal dendrites? Neuroscience 7:2813–27 Lillegraven, J.A. 1979 Reproduction in Mesozoic mammals. In Mesozoic Mammals: The First Two–Thirds of the Mammalian History, eds. J.A. Lillegraven, Z. Kielan–Javorowska, W.A. Clemens, pp. 259–76. Berkeley, Calif. University of California Press Lubbock, J. 1858. Variability of the nervous system. Proc. R. Soc. Lond. 9:480–86 Macagno, E.R., Lopresti, V., Levinthal, C. 1973. Structure and development of neuronal connections in isogenic organisms: Variation and similarities in the optic system of Daphnia magna. Proc. Natl. Acad. Sci USA 70:57–61 Macagno, E.R. 1979. Cellular interactions and pattern formation in the development of the visual system of Daphnia magna (Crustacea, Branchiopoda). I. Interactions between embryonic retinular fibers and laminar neurons. Dev. Biol. 73:206–38 Macagno, E.R. 1980. Number and distribution of neurons in leech segmental ganglia. J. Comp. Neurol. 190:283–302 Maheras, H.M., Pollack, E.D. 1985. Quantitative compensation by lateral motor column neurons in response to four functional hindlimbs in a frog tadpole. Dev. Brain Res. 19:150–54 Mallet, J., Huchet, M., Pougeois, R., and Changeux, J.P. 1976. Anatomical, physiological and biochemical studies on the cerebellum from mutant mice. III. Protein differences associated with the weaver, staggerer and nervous mutation. Brain Res. 103:291–312 Mallouk R.S. 1975 Longevity in vertebrates is proportional to relative brain weight. Fed. Proc. 34: 2102–3 Mallouk, R.S. 1976 Author's reply (to: Aging in vertebrates: Allometric considerations of spleen size and lifespan by W.A. Calder III). Fed. Proc. 35: 97–98 Mangold–Wirz, K. 1966. Cerebralisation und Ontogenesemodus bei Eutherien. Acta Anat. 63:449–508 Mann, M.D., Towe, A.L. Glickman, S.E. 1986. Relationship between brain size and body size among Myomorph rodents. Soc. Neurosci Abs. 12:111 Mariani, J., Crepel,F., Mikoshiba, K., Changeux, J.P., and Sotelo, C. 1977. Anatomical, physiological and biochemical studies of the cerebellum from reeler mutant mouse. Phil. Trans. R. Soc. (Lond.) 281:1–28 Martin, R.D. 1981. Relative brain size and basal metabolic rate in terrestrial vertebrates. Nature 293: 57–60 Martin, R.D., Harvey, P.H. 1985. Brain size allometry. Ontogeny and Phylogeny. In Size and Scaling in Primate Biology. ed. W.L. Jungers. pp. 147–73. New York: Plenum Martini, E. 1912. Studien uber die Konstanz histologischer Elemente. III. Hydatima senta. Z. wiss. Zool. 102:425–645 Maurin, Y, Berger, B., Le Saux, F., Gay, M., Baumann, N. 1985. Increased number of locus ceruleus noradrenergic neurons in the convulsive mutant Quaking mouse. Neurosci. Lett. 57:313–18 Mayr, E. 1963. Animal Species and Evolution. Cambridge, Mass.: Belknap Press of Harvard Univ. Press McLoon, S., C. 1982 Alternation in precision of the crossed retinotectal projection during chick development. Science 215: 1418–20 Mellon Jr., D., Tufty, R.H., Lorton, E.D. 1976. Analysis of spatial constancy of oculomotor neurons in the crayfish. Brain Res. 109:587–94 Meyer, M.P., Morrison, P. 1960. Tissue respiration and hibernation in the thirteen–lined ground–squirrel, Spermophilus tridecemlineatus. Bull. Museum Comp. Zoo. 124:405–21 Miale, I.L., Sidman, R.L. 1961. An autoradiographic analysis of histogenesis in the mouse cerebellum. Exp. Neurol. 4:277–96 Mos, W., Williamson, R. 1986. A quantitative analysis of the spinal motor pool and its target muscle during growth in the Dogfish, Scyliorhinus canicula. J. Comp. Neurol. 248:431–40 Mullen, R.J. 1977 Site of gene action and Purkinje cell mosaicism in pcd<–>normal chimeric mice. Nature 270:245–47 Mullen, R.J., Eicher, E.M., Sidman, R.L. 1976 Purkinje cell degeneration. A new neurological mutant in the mouse. Proc. Natl. Acad. Sci. USA 73: 208–12 Mullen, R.J. and Herrup, K. (1979) Chimeric analysis of mouse cerebellar mutants. In: Neurogenetics: A Genetic Approach to the Central Nervous System. ed., X.O. Breakefield, pp. 271–97. New York: Elsevier–North Holland Muller, K.J., Nicholls, J.G., Stent, G.S. 1982. Neurobiology of the Leech. New York: Cold Spring Harbor Press Munk, O. 1966. Ocular degeneration in deep–sea fishes. Galathea Report, Scientific results of the Danish deep–sea expedition round the world 1950–52, 8:22–31 Narayanan, C.H., and Narayanan, Y. 1978. Neuronal adjustments in developing nucleus centers of the chick embryo following transplantation of an addition optic primordium. J. Embryol. Exp. Morph. 44:53–70 Newman, H.H., Patterson, J.T. 1911. The limits of hereditary control in armadillo quadruplets: A study of blastogenic variation. J. Morph. 22:855–926 Newport, J., Kirschner, M. 1982 a. A major developmental transition in early Xenopus embryos I. characterization and timing of cellular changes at the midblastula stage. Cell 30:675–86 Newport, J., Kirschner, M. 1982 a. A major developmental transition in early Xenopus embryos II. Control of the onset of transcription. Cell 30:687–96 Nicholson, J. L., Altman, J. 1972. The effects of early hypo– and hyperthyroidism on the development of rat cerebellar cortex. I. Cell proliferation and differentiation. Brain Res. 44:13–23 Nieto–Sampredro, J., Saneto, R.P., De Vellis, J., Cotman, C.W. 1985. The control of glial populations in brain: Change in astrocyte mitogenic and morphogenic factors in response to injury. Brain Res. 343: 320–28 Nordeen, E.J., Nordeen, K.W., Sengelaub, D.R., Arnold, A.P. 1985. Androgens prevent normally occurring cell death in a sexually dimorphic spinal nucleus. Science 229:671–673. Nordlander, R.H., Edwards, J.S. 1969. Postembryonic brain development in the monarch butterfly. II. The optic lobes. Wilhelm Roux Arch. Dev. Biol. 163:197–220 Ogawa, F. 1939. The nervous system of earthworm (Pheretima communissima) in different ages. Sci. Rep. Tohoku Univ. [Med]. 13:395–488. Okado, N., Oppenheim, R.W. 1984. Cell death of motoneurons in the chick embryo spinal cord. IX. The loss of motoneurons following removal of afferent input. J. Neurosci. 4: 1639–52 O'Leary, D.D.M., Fawcett, J.W., Cowan, W.M. 1986. Topographic targeting errors in the retinocollicular projection and their elimination by selective ganglion cell death. J. Neurosci. 6:3692–3705 Oppenheim, R.W. 1986. The absence of significant postnatal motoneuron death in the brachial and lumbar spinal cord of the rat. J. Comp. Neurol. 246: 281–286. Oppenheim, R.W. 1987. Cell death during neural development. In Handbook of Physiology, Neuronal Development, Vol 1. ed. W.M. Cowan. in press, Washington, D.C.: American Physiological Society (ultimately published in Ann. Rev. Neurosci. 1989 or 1990) Pakkenberg B, Gundersen HJG (1997) Neocortical neuron number in humans: effect of sex and age. J. Comp. Neurol. 384:312–320. Perkins, C.S., Aguayo, A.J., Bray, G.M. 1981. Schwann cell multiplication in Trembler mice. Neuropath. Appl. Neurobiol. 7:115–26 Pilar, G., Landmesser, L., Burstein, L. 1980. Competition for survival among developing ciliary ganglion cells. J. Neurophysiol. 43:233–254 Pond, C.M. 1977. The significance of lactation in the evolution of mammals. Evolution 31:177–99 Potten, C.S., Wichmann, H.E., Loeffler, M., Dobek, K., Major, D. 1982. Evidence for discrete cell kinetic subpopulations in mouse epidermis based on mathematical analysis. Cell Tiss. Kinet. 15: 305–29 Prestige, M.C. 1970. Differentiation, degeneration, and the role of the periphery: Quantitative considerations. In The Neurosciences, Second Study Program, F.O. Schmitt, ed. pp. 73–82. New York. Rockerfeller Univ. Press Provis, J., van Driel, D., Billson F.A., Russel, P. 1985. Human fetal optic nerve: Overproduction and elimination of retinal axons during development. J. Comp. Neurol. 238:92–101 Purves, D., Rubin, E., Snider, W.D., and Lichtman, J. 1986. Relation of animal size to convergence, divergence, and neuronal number in peripheral sympathetic pathways. J. Neurosci. 6:158–63 Quigley, H.A., Addicks, E.M., Green, W.G. 1982. Optic nerve damage in human glaucoma. III. Quantitative correlation of nerve fiber loss and visual field defect in glaucoma, ischemic neuropathy, papilledema, and toxic neuropathy. Arch. Ophthalmol. 100:135–46 Quinn, L.S., Holtzer, H., Nameroff, M. 1984 Age dependent changes in myogenic precursor cell compartment sizes. Evidence for the existence of a stem cell. Exp. Cell Res. 154: 65–82 Quinn, L.S., Holtzer, H., Nammeroff, M. 1985 Generation of chick skeletal muscule cells in groups of 16 from stem cells. Nature 313:692–94 Quinn, L.S., Nameroff, M. 1983a. Analysis of the myogenic lineage in chick embryos. III. Quantitative evidence for discrete compartments of precursors cells. Differentiation 24:111–23 Quinn, L.S., Nameroff, M. 1983b. Analysis of the myogenic lineage in chick embryos. IV. Effects of conditioned medium. Differentiation 24:124–30 Quinn, L.S., Nameroff, M. 1986. Evidence for a myogenic stem cell. In Molecular Biology of Muscle Development. UCLA Symposia on Molecular and Cellular Biology. New Series. Volume 29. eds. Emerson, C., Fischman, D.A., Nadal–Ginard, B., Siddiqui, M.A.Q., pp. 35–45. New York: Alan R. Liss Raff, M.C., Hornby–Smith, A., Brockes J.P. 1978. Cyclic AMP as a mitogenic signal for cultured rat Schwann cells. Nature 273:672–73 Rager, G. 1980 Development of the retinotectal projection in the chicken. Adv. Anat. Embryol. Cell Biol. 63: 1–92 Rakic, P. 1985. Limits of neurogenesis in primates. Science 227:1054–56 Rakic, P., Riley, K.P 1983a. Overproduction and elimination of retinal axons in the fetal rhesus monkey. Science 219:1441–44 Rakic, P., Riley, K.P. 1983b. Regulation of axon number in primate optic nerve by prenatal binocular competition. Nature 305: 135–137 Raymond, P.A. Reifler, M.J., Rivlin, P.K. and Clendening, B. 1986. Progenitor cells specific for rods lose their specificity in regenerating goldfish retina. Soc. Neurosci Abst. 12:118 Reh, T.A., Tully, T. 1986. Regulation of tyrosine hydroxylase–containing amacrine cell number in larval frog retina. Devel. Biol. 114:463–469 Ricklefs, R.E., Marks, H.L. 1984. Insensitivity of brain growth to selection of four–week body mass in Japanese quail. Evolution 38:1180–85 Rodieck, R.W., Brening, R.K. 1983. Retinal ganglion cells: Properties, types, genera, pathways and trans–species comparisons. Brain Behav. Evol. 23:121–164 Romanes, G.J. 1946. Motor localization and the effects of nerve injury on the ventral horn cells of the spinal cord. J. Anat. 80:117–31 Sacher, G.A., Staffeldt, E.F. 1974. Relation of gestation time to brain weight for placental mammals: Implications for the theory of vertebrate growth. Amer. Natur. 108:593–615. Salzer J.L., Bunge, R.P., Glaser, L. 1980. Studies of Schwann cell proliferation. III. Evidence for the surface localization of the neurite mitogen. J. Cell Biol. 88:767–78 Sanes, J.R., Rubenstein, J.L.R., Nicolas J–F. 1986. Use of a recombinant retrovirus to study post–implantation cell lineage in mouse embryos. EMBO J. 5:3133–42 Satorre, J., Cano, J., Reinoso–Surez, F. 1986. Quantitative cellular changes during postnatal development of the rat dorsal lateral geniculate nucleus. Anat. Embryol. 174:321–27 Schoenwolf, G.C. 1985. Shape and bending of the avian neuroepithelium: Morphometric analyses. Dev. Biol. 109:127–39 Shankland, M., Weisblat, D.A. 1984. Stepwise commitment of blast cell fates during the positional specification of the O and P cell lines in the leech embryo. Devel. Biol 106:326–42 Shariff, G.A. 1953. Cell counts in the primate cerebral cortex. J. Comp. Neurol. 98:381–400 Sholl, D. 1948. The quantitative investigation of the vertebrate brain and the applicability of allometric formulae to its study. Proc. R. Soc. Lond. 135:243–58 Shook, B.L., Maffei, L., Chalupa, L.M. 1984. Functional organization of the cat's visual cortex after prenatal interruption of binocular interactions. Proc. Natl. Acad. Sci. USA 82:3901–5 Sidman, R.L., Lane, P.W., and Dickie, M.M. 1962. Staggerer, a new mutation in the mouse affecting the cerebellum. Science 137:610–12 Silver, J., Hughes, A.F.W. 1974. The relationship between morphogenetic cell death and the development of congenital anophthalmia. J. Comp. Neurol. 157:281–302 Silver, J. 1978. Cell death during development of the nervous system. In Handbook of Sensory Physiology Vol. IX. ed. M. Jacobson. pp. 419–436. New York: Springer Verlag. Sonmez, E., Herrup, K. 1984. Role of staggerer gene in determining cell number in cerebellar cortex. II. Granule cell death and persistence of the external granule cell layer in young mouse chimeras. Dev. Brain Res. 12:271–283. Spitzka, E.A. 1903 Brain weights of animals with special reference to the weight of the brain in macaque monkey. J. Comp. Neurol. 13: 9–17 Stephan, H. 1958. Vergleichend–anatomische Untersuchungen an Insektivorengehirnen. Morphol. Jahrb. 99:853–80 Sternberg, P.W., Horvitz, H.R. 1984. The genetic control of cell lineage during nematode development. Ann. Rev. Genet. 18:489–524 Stewart, R.R., Spergel, D., Macagno, E.R. 1986. Segmental differentiation in the leech nervous system: The genesis of cell number in the segmental ganglia of Haemopis marmorata. J. Comp. Neurol. 253:253–59 Stewart, R.R., Gao, W.–Q., Peinado, A., Zipser, B., Macagno, E.R. 1987 Cell death during gangliogenesis in the leech: Bipolar cells appear and then degenerate in all ganglia. J. Neurosci. 7:1919–27 Stone, J. 1983. Parallel Processing in the Visual System. The Classification of Retinal Ganglion Cells and its Impact on the Neurobiology of Vision. Plenum Press, New York Storrs, E.E., Williams, R.J. 1968. A study of monozygous quadruplet armadillos in relation to mammalian inheritance. Proc. Natl. Acad. Sci. USA 60:910–14 [Strom, R.C., Williams, R.W. 1998. Cell production and cell death in the generation of variation in neuron number. J. Neurosci. In press. Aug98RW] Studnicka, F.K. 1905. Die Parietalorgane. In Lehrbuch der vergleichende mikroskopischen Anatomie der Wirbeltiere. A. Oppel, ed. vol. 5. S.G. Fischer Verlag, Jena. Sulston, J.E. 1976. Post–embryonic development in the ventral cord of Caenorhabditis elegans. Phil. Trans. R. Soc. Lond. Ser. B. 275:287–97 Sulston, J.E., Horvitz, H.R. 1977. Post–embryonic cell lineages of the nematode Caenorhabditis elegans. Devel. Biol. 56:110–156 Tanaka, H., Landmesser, L.T. 1986a. Interspecies selective motoneuron projection patterns in chick–quail chimeras. J. Neurosci. 6:2880–88 Tanaka, H., Landmesser, L.T. 1986b. Cell death of lumbosacral motoneurons in chick, quail, and chick–quail chimera embryos. A test of the quantitative matching hypothesis of neuronal cell death. J. Neurosci. 6:2889–99 Tåning, ÅA.V. 1950 Influence of the environment on number of vertebrae in teleostean fishes. Nature 165: 28 Taylor, B.A. 1971. Genetic relationships between inbred strains of mice J. Heredity 63:83–86 Temple, S., Raff, M.C. 1986 Clonal analysis of oligodendrocyte development in culture: Evidence for a developmental clock that counts cell divisions. Cell 44: 773–79 Thoenen, H. and Barde, Y.A. 1980. Physiology of nerve growth factor. Phys. Rev. 60:1284–1335 Thoenen, H., Korsching, S., Heumann, R., and Acheson, A. 1985. Nerve Growth Factor. Ciba Fndn. Symp. 116:113–28 Tower, D.B. 1954. Structural and functional organization of mammalian cerebral cortex: The correlation of neurone density with brain size. J. Comp. Neurol. 101:19–52 Torrence, S.A. 1983. Ascidian larval nervous system: Anatomy, ultrastructure, and metamorphosis. Ph.D. thesis, University of Washington, Seattle Trent, C., Tsung, N. Horvitz, H.R. 1983. Egg–laying defective mutants of the nematode Caenorhabditis elegans. Genetics 104:619–47 Truman, J.W. 1983. Programmed cell death in the nervous system of an adult insect. J. Comp. Neurol. 216:445–52. Truman, J.W. 1984. Cell death in invertebrate nervous systems. Ann. Rev. Neurosci. 7:171–88 Turner, D.L, Cepko, C.L 1987. A common progenitor for neurons and glia persists in rat retina late in development. Nature 328: 131–36 van Essen, D.C. Newsome, W.T., Maunsell, J.H.R. 1984. The visual field representation in striate cortex of the macaque monkey: Asymmetries, anisotropies, and individual variability. Vision Res. 24:426–48 van Essen, D.C., Newsome, W.T, Maunsell, J.H.R., Bixby, J.L. 1986. The projections from striate cortex (V1) to areas V2 and V3 in the macaque monkey: Asymmetries, areal boundaries and patchy connections. J. Comp. Neurol. 244:451–80. Vernon, J.A., Butsch, J. Effect of tetraploidy on learning and retention in the salamander. Science 125:1033–34. von Szily, A. 1912 Uber die einleitenden Vorgänge bei der ersten Entstehung der Nervenfasern im N. opticus. Albrecht von Graefe's Archiv. f. Ophthal. 81:67–86, plates 5 and 6. Waddington, C.J. 1942 Canalization of development and the inheritance of acquired characters. Nature 150: 563–65 Ware, R.W., Clark, D., Crossland, K., Russell, R.L. 1975 The nerve ring of the nematode Caenorhabditis elegans. Sensory input and more output. J. Comp. Neurol. 162: 71–110 Weisblat, D.A., Harper, G., Stent, G.S., Sawyer, R.T. 1980. Embryonic cell lineages in the nervous system of the Glossiphoniid leech Helobdela triserialis. Dev. Biol. 76:58–78. Weisblat, D.A., Sawyer, R.T., Stent, G.S. 1978. Cell lineage analysis by intracellular injection of a tracer enzyme. Science 202:1295–98. Weisblat D.A., Blair, S.S. 1982 Cell lineage in leech neurogenesis during normal development and after the ablation of identified blastomeres. NRP Bull. 20:783–93. Wetts, R., Herrup, K. 1982. Interaction of granule, Purkinje and inferior olivary neurons in lurcher chimeric mice. II. Granule cell death. Brain Res. 250:358–362. Wetts, R. and Herrup, K. 1983. Direct correlation between Purkinje and granule cell number in the cerebella of lurcher chimeras and wild–type mice. Dev. Brain Res. 10:41–47. White, J., Southgate, E., Thomson, J.N., Brenner, S. 1976 The structure of the ventral nerve cord of Caenorhabditis elegans. Phiolos. Trans. R. Soc. Lond. Ser. B 275: 327–48 Whitington, P.M., Bate, M., Seifert, E., Ridge, K., Goodman, C.S. 1982. Survival and differentiation of identified embryonic neurons in the absence of their target muscles. Science 215:973–75. Williams, R.W., Bastiani, M.J., Lia, B., Chalupa, L.M 1986. Growth cones, dying axons, and developmental fluctuations in the fiber population of the cat's optic nerve. J. Comp. Neurol. 246:32–69. Williams, R.W., P. Rakic 1988a. Elimination of neurons from the lateral geniculate nucleus of rhesus monkeys during development. J. Comp. Neurol. 272: 424–436. Williams, R.W., P. Rakic. 1988b. Three–dimensional counting: An accurate and direct method to estimate the number of cells in sectioned material. J. Comp. Neurol. 278: 344–52. Williams, R.W., Ryder, K., Rakic, P. 1987. Emergence of cytoarchitectonic differences between areas 17 and 18 in the developing rhesus monkey. Soc. Neurosci. Abstr. 13: 1044. [Williams, R.W. 2000. Mapping genes that modulate brain development: a quantitative genetic approach. In: Mouse brain development (Goffinet AF, Rakic P, eds). Springer Verlag, New York, pp 21Ð49.] Wilson M.A. 1971. Optic nerve fibre counts and retinal ganglion cell counts during development of Xenopus laevis (Daudin). Quart. J. Exp. Physiol. 56:83–91. Wimer, R.E., Wimer, C.C., Vaughn, J.E., Barber, R.P., Balvanz, B.A., Chernow, C.R. 1976. The genetic organization of neuron number in Ammon's horns of house mice. Brain Res. 118:219–43. Wingert, F. 1969. Biometrische Analyse der Wachstumsfunktionen von Hirnteilen und Körpergewicht der Albinomaus. J. Hirnforsch. 11:133–97. Winklbauer, R., Hausen, P. 1983. Development of the lateral line system in Xenopus laevis. III. Cell multiplication and organ formation in the supraorbital system. J. Embryol. Exp. Morphol. 76: 283–296 Wright, S. 1978. Evolution and the Genetics of Populations. Vol. 4: Variability within and among Natural Populations. The University of Chicago Press, Chicago Yablokov, A.V. 1974.Variability of Mammals. New Delhi, Amerind Publishing Co Young, J.Z. 1971. The Anatomy of the Nervous System of Octopus vulgaris. Oxford; Clarendon Press. Zamenhof, S. 1941 Stimulation of the proliferation of neurons by the growth hormone. I. Experiments on tadpoles. Growth 5:123–39 Zamenhof, S. 1942 Stimulation of cortical cell proliferation by the growth hormone. III. Experiments on albino rats. Physiol. Zool 15:281–92 Zamenhof, S. Mosley, J., Schuller, E. 1966. Stimulation of the proliferation of cortical neurons by prenatal treatment with growth hormone. Science 152:1396–97 Zamenhof, S. Mosley, J., Schuller, E. 1971. Prenatal cerebral development: Effects of restricted diet, reversal by growth hormone. Science 174: 954–55     Footnote 1. For a particular vivid example of the limitation of this single variable approach, see the controversy surrounding the correlation between brain size and longevity (Mallouk, 1975, 1976, Clader 1976). RETURN TO TEXT. Footnote 2. The only instance we are aware of in which an increase in neuron number may be maladaptive is the case of the mutant mouse quaking. Maurin et al (1985) have reported that the number of noradrenergic neurons in the locus coeruleus of quaking is about 20% above normal. This increase is associated with convulsion. RETURN TO TEXT. Footnote 3. This may be particularly true at early stages of development. As Martin (1981) has argued persuasively, the amount of energy that can be transferred from parent to offspring may set an upper limit to brain size. The advent of fully functional lactation in mammals before the end of the Triassic period was undoubtedly a key innovation that enabled mammals to sustain relatively large populations of neurons and glial cells (Pond 1977, Lillegraven 1979), and this in turn may have contributed significantly to the rapid radiation of mammals during the early Cenozoic. Speciation rates in mammalian genera are estimated to be about five times higher than rates in lower vertebrate genera (Bush et al 1977). The rate of growth of mammalian young that possess particularly large brains is often slow, and gestation and maturation take a long time (Sacher & Staffeldt 1974). We see this pattern clearly in primates (Gould 1977, p. 367), but it is also apparent in other mammals. For instance, the nectar-feeding bat, Glossophaga sorichina, has a very high brain/body weight ratio, and Eisenberg (1981, p. 307) points out that the young may develop slowly principally because the milk contains little fat. This strategy allows the mother to defray the cost of building a new brain over a longer period. In general, animals with big brains have small litters, slow development, and intense parental care. RETURN TO TEXT. Footnote 4. Hamburger (1975) has pointed out, however, that the overproduction of spinal motoneurons cannot be ascribed to an imprecise programming of the number of mitotic cycles. He observed that the total number of spinal motor neurons produced before the onset of neuron death in a number of 5.5- and 6-day chicken embryos was relatively constant. (range from 18,900 to 21,600, n = 11). RETURN TO TEXT.   Since 11 August 98

Neurogenetics at University of Tennessee Health Science Center

Print Friendly

Top of Page

Home Page  |  Genome DBs  |  Phenome DBs  |  Publications  |  People & Associates
Mouse Brain Library  |  Related Sites  |  Complextrait.org

Nervenet.org  |   MBL.ORG

Robert W. Williams | Alex Williams © 2002, Nervenet.org