|
| |||||
|
| ||||||||
|
| ||||||||
Home  Publications Publications |
|
|
Note to the Reader Quantitative Neuroanatomy: A Picture is Worth a Thousand Words, but a Number is Worth a Thousand Pictures. Organizers: John H. Morrison and Patrick R. Hof Society for Neuroscience Education Committee Saturday, November 7, 1998 (2:30–3:00 pm) Westin Bonaventure Hotel and Suites, Los Angeles, CA pp. 66–78.
Print Friendly |
Word Document
Contents Quantitative methods now pervade most aspects of neuroanatomical
research, whether the focus is on dendritic spines or the topography of
human neocortex. Sophisticated techniques to study cells in the CNS have
gained in importance as the field of neuroanatomy has matured beyond
qualitative analysis. Efficient methods to quantify cells in thick or thin
sections, particularly direct three-dimensional counting (Williams & Rakic,
1988) and several adaptations of the disector (Gundersen et al., 1988),
make it easier to obtain unbiased estimate of neuroanatomical traits. As a
practical matter, the most important advance in quantitative techniques has
been the rapid hybridization of microscopes, video systems, fast
microcomputers, and powerful application programs such as NIH Image (http://rsb.info.nih.gov/nih-image/Default.html).
These advances have given neuroscience a major boost, and investigators can
now use more trustworthy quantitative techniques to study large numbers of
cases. The promise of quantitative genetics. This tutorial
illustrates how to exploit quantitative neuroanatomical datasets to map and
positively identify (clone) genes that generate the astonishing, but
nonetheless normal, variation in CNS architecture. The types of genes that I
am referring to are called quantitative trait loci or QTLs, and these
QTLs are responsible for much of the inheritable variation among individuals
within a species. For example, the volume and number of cells in visual
cortex of humans and other primates vary nearly 3-fold (Gilissen & Zilles,
1996; Suner & Rakic, 1996), and most of this remarkable variation is
generated by sets of still completely unknown neurogenic QTLs. You don't
need expertise in molecular biology to map these genes. In the near future
it should even be possible to clone QTLs without running gels. A solid
background in statistics and expertise in phenotyping is more helpful at
present than expertise in molecular biology. What you must have to pursue
complex trait analysis to study the nervous system is the ability, patience,
and resources to quantify large numbers of cases. The QTL methods I describe in this paper have become available only in
the last few years (Tanksley, 1993; Lander & Schork, 1994, Kearsey & Pooni,
1996) and their applications in neuroscience are still largely restricted to
mice and human populations. These methods depend on the polymerase chain
reaction (PCR), high-density genetic maps, and sophisticated statistics
programs. The application of these methods in the next decades will
revolutionize our understanding of normal genetic mechanisms controlling CNS
development, susceptibility to disease, and even CNS evolution (Williams
2000; Greenspan 2001). Progress in QTL mapping is just as relentless as
in any other branch of genetics, and the application of new methods will
soon allow reseachers to achieve extremely high precision QTL
mapping—precision of better than 0.2 cM—with relatively modest total
phenotyping requirements and no genotyping at all within the next ten years
(cf., Williams et al., 2001).
The terrific feature of these new genetic tools is that specific categories
of genes can be targeted for analysis using a forward genetic approach. A
forward genetic approach starts with well-defined phenotypes and moves
toward single genes that contribute to those phenotypes (Takahashi et al.,
1994). It is therefore an ideal approach for neuroscientists, who typically
begin with specific problems and questions about specific CNS traits.
Forward genetics is not fishing; instead it is highly directed, like
harvesting fruit from a chosen tree in an orchard. The genes discovered
using QTL methods will usually be key controllers in molecular pathways that
normally influence CNS traits. This chapter summarizes key principles and methods involved in a
quantitative genetic dissection of the mouse CNS. After reading this chapter
you may be interested in several papers that provide concrete examples of
how and why we are using these methods to map genes that control variation
in neuron number. A set of closely related papers on this topic (covering
olftactory bulb, striatum, hippocampus, and cerebellum) are available
without restriction on this web site and at
www.jneurosci.org/cgi/content/full/16/22/7193,
www.jneurosci.org/cgi/content/full/18/1/138, and
www.jneurosci.org/cgi/content/full/16/22/7193. A more general overview
of the genetics of brain weight is available at
http://www.nervenet.org/papers/BrainRev99.html. What are QTLs? Quantitative trait loci are normal genes in every
sense of the word, but they are referred to using this somewhat unwieldy
term to highlight the fact that variant forms—or alleles—of QTLs have
relatively subtle quantitative effects on phenotypes (Lynch & Walsh, 1998).
In studies of human populations in clinical settings, QTLs are also referred
to as susceptibility genes, because humans who carry certain alleles are at
greater risk of developing disease. QTLs are often contrasted with Mendelian
loci that have pronounced, and usually discontinuous, qualitative effects on
phenotypes, but there is actually no sharp demarcation between quantitative
and qualitative traits. QTLs that have particularly large effects that verge
on producing Mendelian segregation patterns (e.g., 1:2:1) are major-factor
or major-effect QTLs. Their large effects make them the easiest QTLs to map.
Conversely, allelic variants at Mendelian loci can have graded effects, and
given a particular population or environment, they are also QTLs. The effect
size of a QTL is not in any way a measure of the importance of a gene in a
biological process or network; in fact some of the most important genes may
have only minor sequence variants. In some instances a QTL may encompass two or more polymorphic genes that
are close to each other on a chromosome. "Close" in this sense means that
the two neighboring genes that modulate a trait have not been dissociated
sufficiently by recombination events. The collective effect of such linked
genes may be quite striking, and some effort may be required to dissect the
individual contributions of two of more QTLs apart. There are some
statistical short-cuts to help dissociate two polymorphic genes that
contribute to a "single" composite QTL, but the ultimate solution is simply
to use high resolution mapping panels (that is to say, groups of mice that
collectively harbor many recombination events) to resolve one composite QTL
into two or more constituents. An apt analogy is the differences of image
resolution achieved by light and electron microscopes—the higher the
frequency of the light source the better the resolution. In gene mapping,
the greater the number of recombination events, the better the resolution.
The ultimate goal is of course to resolve the effects of the single genes
that underlie QTLs; to turn QTLs into QTGs (quantitative trait genes) or
even QTNs (quantitative trait nucleotides). Four conditions. Methods used to map QTLs affecting the nervous
system can be applied widely, with the following provisions: "The importance of phenotype definition and delineation cannot be
overemphasized. For what we refer to now as "gene mapping" is actually
"phenotype mapping," with identificaiton of new gene loci merely a
by-product in our current age of ignorance. After the year 2005, when most
functional loci in the human genome will have been mapped and sequenced,
there will still remain huge gaps in our knowledge about
genotype-phenotype correlations. So as long as there is interest in
identifying alleles that cause human phenotypes, there will be continuing,
long-term interest in phenotype mapping." (from A. S. Aylsworth, 1998) Sources of variance. Variation in the value of a trait or
phenotype is often thought of as an experimental annoyance. However, when
the aim is to map QTLs, the greater the genetic variance, the better the
prospects of success (Figure 1). The variance that is initially
measured in a quantitative neuroanatomical study (the square of the standard
deviation) has many sources (Falconer & Mackay, 1996; Lynch & Walsh, 1998,
chapters 5–7). For this reason, one of the first steps in a QTL analysis is
to partition this variance into its major components. Three especially
important components are (1) technical and sampling variance (Vt),
(2) environmental variance (Ve), and (3) additive genetic variance (Va).
There are several ways to separate them (Williams et al., 1996). Technical error. Technical error can be estimated by repeated
analysis of a subset of cases. In one recent study, we used a quantitative
electron microscopic method to count retinal ganglion cells in mice. To
estimate the reliability of this method, we simply recounted cases (Williams
et al., 1996). Most cases were rephotographed and recounted by different lab
members to estimate inter-observer reliability. We discovered that technical
errors in our study were as important a source of variance as all
environmental sources of variance combined. In this study to get a reliable
strain average, we had to increase the number of cases to about 6 to 8
animals. Environmental and non-genetic developmental variance can be estimated by
phenotyping related individuals. For example, in (Figure A) the
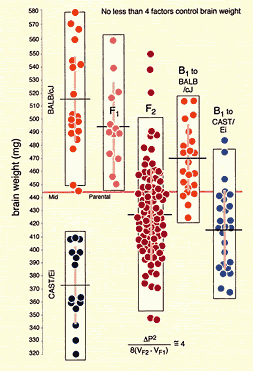
variability in brain weight among BALB/cJ individuals is entirely due to
environmental differences and technical error. Once technical errors have
been factored out, the variance among inbred mice within a strain is almost
purely environmental and is a good estimate of Ve. Variation in age,
sex, body weight, litter size, age of mother and parity of her litters,
exposure to pathogens, temperature and humidity variation, the sometimes
amazing differences from bag to bag in non-synthetic mouse chows from major
vendors (Michael Tordoff of the
Monell
Chemical Senses Center finds 10-fold variation in calcium content between
bags), seasonal fluctuation in water quality, and a host of other
environmental factors can often be minimized or carefully controlled in
studies using mice. Failure to control for these factors can and will give
rise to variation within colonies and between laboratories. For studies of
robust Mendelian and quantitative traits, these sources of variation may not
matter much, but if you are trying to track down a host of genes that affect
the kinetics of neurogenesis in the hippocampus or of a sensitive behavioral
trait then go to the effort to control as much as possible. For example, if
practical feed animals a more expensive but much less variable synthetic
chow and provide your colony with a consistent source of deionized water. (Box
1: The challenge of keeping records provides advice on building and
maintaining a coherent and accurate laboratory database.) What we are left
with after accounting for technical and environmental sources of variance is
a large amount of unexplained or 'residual' variance. This is the genetic
variance that we will be trying to split apart into a neatly defined set of
precisely mapped QTLs. Comparing strains. Before mapping QTLs, we need to know that the
trait is variable and that the variation is heritable. An easy way to go
about this is to phenotype 5–10 individuals from each of 10 or more common
inbred strains of mice, all raised in the same colony under closely matched
conditions. It is a good idea to gather cases from several different
litters. If all mice of a particular strain come from a single litter, then
the variance between strains could have as much to do with the health and
experience of the mother as with her genotype. In our electron microscopic study of ganglion cells, we found that 70–80%
of the variance was heritable. Heritability, defined broadly to include all
sources of genetic variance, was estimated by comparing levels of variance
within and among 17 inbred strains. The average variance within a strain,
Vw, was 13.7 (variance units are x106cells2).
When the technical error, Vt, was subtracted, the average
environmental variance, Ve, was reduced to 4.65. In comparison, the
additive genetic variance, Va, computed across strains was 27.9. From
these values we computed the broad heritability, h2,
using the equation h2 = 0.5Va / (0.5Va+Ve) (Hegmann
& Possidente, 1981). Substituting values, heritability was estimated to be ~0.75—a relatively
high value, but one that will probably be typical of many quantitative
neuroanatomical traits (Wimer & Wimer, 1989). Selecting strains. Which inbred strains or isogenic F1 hybrids
are appropriate for a preliminary analysis of the heritability of a variable
CNS trait in mice? My suggestions for an initial screen are in approximate
order of priority:
I have chosen these strains for four reasons: (1) most are readily available, (2) these strains differ greatly in both phenotypes and genotypes, (3) their genomes have been characterized extensively, and (4) many of these strains have been used to generate recombinant inbred strains that are proving to be especially useful to neurogeneticists. Some of these mice will not be suitable for certain studies–for example, C3H/HeJ, CBA/J, and SWR/J all carry the mutant rd1 allele of the Pdeb gene that causes photoreceptor degeneration, so none would not be appropriate for an analysis of retinal cell populations. For an excellent synopsis of strains of mice that are suitable for different types of neurogenetic/behavioral analysis see Crawley et al. (1997) Level of genetic variation between strains. One key to successfully mapping QTLs is a high level of genetic variation among mice. Many strains listed above have now been genotyped ~6400 loci (Dietrich et al., 1994). It is therefore possible to determine at an early stage how feasible it will be to map QTLs using a cross between any two of these strains. For most pairs of strains, more than 30% of marker loci have reliable and easily scored differences (Fig. 1). In contrast, it would not be practical to map QTLs responsible for the heritable 100 mg difference in brain weight between BALB/cJ and BALB/cByJ because these strains are closely related, and just finding suitable marker loci would be a major undertaking. In this particular case a complementary analysis of differences in expression levels of genes or proteins might be extremely fruitful (Sandberg et al., (2000)).
Using multiple regression analysis to improve specificity of QTL mapping. Quantitative neuroanatomical methods can be used to generate unbiased estimates, but before these estimates can be employed to map genes, they will need to be fine-tuned using multiple regression techniques (Box 2: Resources for regression analysis). The reason is that a trait may be tightly correlated with other traits, and if care is not taken, it is possible to map the wrong QTLs or no QTLs at all. For example, assume that we are interested in mapping genes that specifically control normal variation in numbers of Purkinje cells in the cerebellum. If we count these neurons in a large sample of animals and use these raw numbers to map QTLs, we will almost certainly, and inadvertently, map genes that affect the entire cerebellum, the entire brain, or perhaps even the entire body. To sidestep this problem, and to map QTLs that have selective effects on Purkinje cells, we need to have data on body, brain, and cerebellar weight. The more data we have on what might be called “higher-order” phenotypes, the better. In this particular example, we should perform a multiple regression analysis of Purkinje cell number against cerebellar weight, brain weight, body weight, sex, age, fixation quality, the identity of the investigator who carried out the dissection and counted the tissue, method of processing, and whatever other parameters we can demonstrate are statistically associated with our estimates of Purkinje cell number. If an individual parameter is not significant in this multiple regression, then it should be eliminated from the analysis. David Airey, Lu Lu, and I carried out an analysis like this, and after stripping away extraneous variance generated by many general factors we were able to map four QTLs that specifically control the size of the mouse cerebellum (Airey et al., 2001). The phenotype values used in this analysis were multiple regression residuals—the differences between expected and observed cerebellar weights. With this background on the genetics of cerebellar size, we are now poised to study particular cell populations within cerebellum. In almost any study of cell number in the nervous system, it will help to factor out global effects. Mapping QTLs that modulate CNS traits
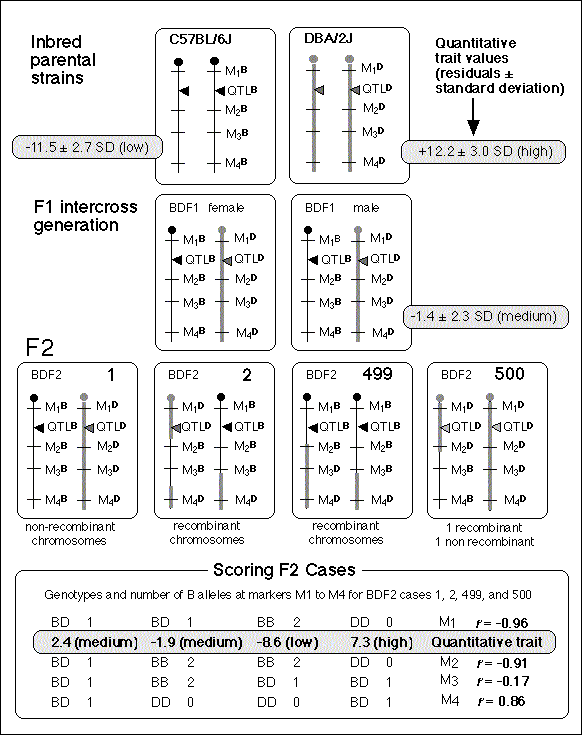
A QTL mapping study is in essence a search for statistically significant associations between variation in a quantitative trait such as Purkinje cell number and variation in genotypes at particular gene loci (Tanksley, 1993). If our aim is to map QTLs using a set of F2 intercross progeny, then we would compare the residuals computed by regression analysis to the genotypes that we have obtained at 70 to 100 marker loci (Fig. 1). To simplify the explanation of how we compare phenotypes and genotypes I will describe a hypothetical experiment and use this experiment to review some useful genetics. It will help those who are unfamiliar with the methods to spend a few minutes looking over Figure 3, which summarizes graphically, much of what follows. The QTL mapping experiment starts with a morphometric analysis of Purkinje cells in two inbred strains of mice: C57BL/6 (B type; named for its black coat color) and DBA/2 (D type; named for its dilute brown coat color). These strains are fully inbred, meaning that alleles at all autosomal gene loci in mice of a given strain are identical. Pairs of chromosomes have precisely the same DNA sequence–imagine each chromosome as a string of 4000 Bs, with each B representing the B-type allele at each of 4000 genes on an average mouse chromosome. Generating an F2 intercross. Assume that Purkinje cells in these two inbred strains have now been counted and that the majority of C57BL/6 mice have low counts (a residual -11,500 ± 2,700, as shown in Fig. 2), whereas the majority of DBA/2 mice have high counts (a residual of +12,300 ± 3,000, as shown in Fig. 2). There isn't much overlap between estimates, and our analysis demonstrates that heritability is high. We mate these mice, producing the first filial or F1 generation of progeny. Individual F1 mice are hybrids with BD genotypes, but these hybrids are also isogenic because each F1 mouse inherits one complete set of B chromosomes from its mother and one complete set of D chromosomes from its father. That is, all F1 offspring have precisely the same BD genotype at all autosomal loci. With the exception of sex differences, the quantitative variation among these F1 animals is purely environmental and technical (Ve + Vt). We breed the F1 mice to generate an F2 generation. Half of the chromosomes packaged into gametes of the F1 mice are themselves hybrids, with long alternating stretches of B and D alleles generated during meiosis by reciprocal crossovers (recombinations) between aligned B and D chromatids. Furthermore, at any autosomal gene locus in the F2 generation, the ratio of BB, BD, and DD genotypes will be close to the expected Mendelian binomial ratio of 1:2:1. Now the total quantitative variation in cell number among F2 progeny is due both to environmental factors—the same environmental factors measured in parental strains and F1s—and to the random segregation of allelic variants at QTLs that affect Purkinje cell numbers. The total variance among F2 progeny—the variance we intend to assign to well-defined QTLs—is simply the total phenotypic variance, Vp, minus Ve + Vt. Linkage and haplotypes. We do not know the genotype of a particular F2 animal at a particular gene locus unless we type that animal's DNA. However, we don't need to sequence or analyze each gene individually. We can infer genotypes of entire chromosomal regions quite reliably by typing only a few marker loci per chromosome. The reason this can be done is that during meiosis there is on average only one crossover per chromosome. In fact, the genetic length of a chromosome is defined by the frequency of recombination. A chromosome that is 50 centimorgans (cM) long experiences an average of one crossover event per meiosis, generating two recombinant chromosomes and two non-recombinant or parental-type chromosomes. (Note that in contrast to genetic length measured in cM units, the physical length of a chromosome is measured in bases or basepairs and because recombination frequencies are quite variable there is only a loose correspondence between physical and genetic lengths.) The closer two neighboring genes are to each other on a chromosome, the less likely it is that they will be separated by a recombination event (Tanksley, 1993). If genes are within 1 centimorgan (cM) of each other (about 2 million basepairs of DNA in mice but only 1 million basepairs in humans), they will be split apart only about 1 in 100 times, and as a result neighboring genes of particular types on a single chromosome (referred to as a haplotype) will tend to stay together from generation to generation. Geneticists refer to this association using the more imposing terms linkage disequilibrium or gametic phase disequilibrium. The greater the disequilibrium, the higher the probability that particular strings of genes or alleles present on a particular chromosome–the haplotype–will be inherited as a non-recombinant or parental-type unit in the F2 progeny. The utility of linkage. This linkage between neighboring genes means that we do not need to analyze every gene in an individual F2 mouse to deduce the probable genotype at a particular locus. In fact, linkage disequilibrium is high enough in an F2 intercross that we can confidently infer the genotype at any of approximately 80,000 genes in the 3 billion basepair (bp) mouse genome by typing only 70 to 100 well-distributed marker loci that collectively sample less than 20,000 bp, or 0.006% of the genome. The closer a particular marker is to a QTL, the better the inference (Weiss and Terwilliger, 2000). A single marker locus will effectively sample a chromosomal interval of about 15 cM on either side. This region is called the marker's swept radius. As few as 3 to 4 markers will sweep an entire chromosome in an F2 intercross. The first aim of QTL mapping is to find one or more marker loci, such as D5Mit294 shown in Figure 2, for which patterns of the three genotypes match those of phenotypes. We hope to find markers that are statistically associated and physically linked to QTLs that modulates 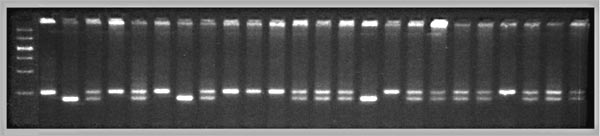 Fig. 2. Genotypes at a microsatellite locus on chromosome 5 (D5Mit294). The left lane is a DNA size standard, and the next two lanes are PCR samples from the parental strains B (higher band at 198 bp) and D (lowest band at 176 bp). Lanes 4 to 25 are the F2 samples. The bottom band—or bands, in the case of heterozygotes—define the genotype of each animal. The bands at the top of the figure are caused by DNA retained in the pipetting wells. Figure from work by G. Zhou (Zhou & Williams, 1997; see Detailed PCR protocols for mapping microsatellites.) Purkinje cell numbers. Given that the parental strain, C57BL/6J, has fewer Purkinje cells, we expect that BB individuals will on average have fewer cells than DD individuals at marker loci linked to important QTLs. But for a trait controlled by as many as 10 or 20 QTLs we can also expect to find markers at which DD individuals have fewer cells. BD heterozygotes will typically have intermediate numbers of cells, but if either the B or D allele at a particular QTL is dominant, then heterozygotes as a group will have either high or low cell number. In a QTL analysis it is important to realize that we are concerned with group means, not individuals. Some BB individuals may have more cells than BD or even DD individuals. In contrast to Mendelian traits, quantitative traits are controlled by numerous genes, and except in unusual circumstances, no single QTL is responsible for more than a relatively small fraction of the phenotypic variance. A major-effect locus may account for 20% of the genetic variance, but values less than 10% are far more common (Tanksley, 1993; Roff, 1997). Environmental and developmental perturbations will also generate exceptional phenotypes. Interval mapping. If a QTL has a small effect or if a QTL has a large effect but is located far from flanking markers, then the statistical association between genotypes and phenotypes will be weak. In either case, we may fail to detect Purkinje cell QTLs (an error of omission, or Type II error). However, we often have data on markers that flank both sides of the QTL. Using genotype data at these flanking markers we can predict the most likely genotypes at any intermediate position between markers and compare these inferred genotypes with Purkinje cell numbers. This can greatly improve our ability to detect QTLs and it also allows us to statistically distinguish between nearby QTLs with small effects and more distant QTLs with large effects. The statistical method used to infer QTL genotypes and then compare them with actual phenotypes is called interval mapping (Lander & Botstein, 1989) Figure 3. See the legend at the bottom of the figure.
Genotyping microsatellite marker loci. We can determine the genotype of each F2 animal by measuring differences in the number of basepairs of DNA in highly variable repeat sequences called microsatellites (Fig. 2). Many thousands of these variable repeat sequences are scattered throughout the mammalian genome. Most microsatellites are in anonymous, non-coding stretches of DNA, but some map within introns, and more rarely, within exons. (This latter group can produce severe neurodegenerative diseases in humans, most notably spinocerebellar ataxia, Friedrich's ataxia, and Huntington's disease.) A set of ~6700 highly polymorphic microsatellites called simple sequence length polymorphisms (SSLPs) have been mapped in mouse by Dietrich et al. (1994). When we say that microsatellites are polymorphic, we simply mean that different strains of mice—in our example, C57BL/6 and DBA/2—have alleles that differ in number of repeats. Fifty-two percent of all microsatellite loci in C57BL/6 and DBA/2 are polymorphic and differ by 2 bp or more (Dietrich et al, 1996). As illustrated in Figure 2, differences in the length of these DNA sequences are easy to detect and score by electrophoresing PCR products through agarose or polyacrylamide gels. The DNA is visualized using a fluorescent DNA–binding dye such as ethidium bromide.
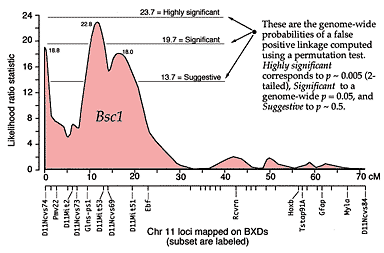
QTLs are defined by strong statistical associations. We are now ready to return to the question posed earlier: how do we compare variation in Purkinje cell number (or any other phenotype) with genotypes in the F2 generation? At any particular gene locus, each F2 animal will have BB, BD, or DD genotypes. In Figure 2, reading from left to right, the first 22 F2 genotypes, starting with lane 4, are HBHBD HBBBH HHDBH HHHBH HH (H for heterozygotes). After all F2s have been genotyped at several markers on each chromosome, we need to evaluate the data and determine the likelihood that we have mapped one or more QTLs to particular chromosomal intervals. Information on several of the programs that are used for this purpose is provided in Box 3: Programs for mapping QTLs. The initial mapping analysis will typically involve what is now referred to as simple interval mapping. Simple interval mapping assumes that we do not already know of any particular QTLs that influence variation in Purkinje cell number. However, if QTLs are successfully mapped in the first round of analysis (see Statistical criteria), then we may advance to composite interval mapping. This refinement is really nothing more than the extension of the multiple regression analysis we have already discussed, but instead of compensating for environmental effects or global variables like body size and brain weight, we compensate for the presence of one or more well defined QTLs. The strength of association between variation in a phenotype and the F2 genotypes at marker loci can be assessed using a F statistic, the logarithm of the odds ratio (the LOD score), the likelihood ratio statistic (LRS), or a conventional probability of linkage. These statistics are interconvertable. LRS scores have a conventional chi-square distribution and are relatively easy to interpret. The LOD score is equal to the LRS divided by 4.61. Both statistics are ratios of probabilities (or likelihoods) that a QTL is, or is not, located within a tested chromosomal interval. But this really does not explain what these statistics are doing. Let me explain the idea using more familiar statistics: analysis of variance (ANOVA), Pearson product-moment correlations, and linear regression. ANOVA. To perform a statistical analysis and to test the likelihood that there is a QTL linked to the locus D5Mit294 in Figure 2 above, we could simply divide cases into categories by genotype and perform a single-factor ANOVA. With two degrees of freedom among the three genotypes and a total of more than 100 progeny, we would need an F statistic above 3 to suspect that D5Mit294 might be linked to a QTL. In our example, we have been fortunate and the F statistic is 9.4, with an associated p of 0.00014. This would seem to be strong evidence that there is a QTL near this marker, but this statistic alone does not tell us much about differences among the genotypes. Correlation and regression. To obtain additional information we could score genotypes by numbers of B alleles: BB = 2, BD = 1, and DD = 0 (computationally, it is sometimes preferable to score genotypes as -1, 0, and +1). It would then be possible to compute a correlation between phenotypes and genotypes to assess the strength of linkage. The correlation in this example is –0.28. The negative sign indicates that B alleles are typically associated with cases that have lower cell numbers. The amount of variance that this putative QTL generates can be estimated by squaring the correlation. In this example, r2, the coefficient of determination, is 0.076. In other words, approximately 7.6% of the variance is associated with a QTL on chromosome (Chr) 5 near D5Mit294. We can also regress phenotype values against genotype values and determine whether the regression coefficient is significantly different from zero. In this case, the slope of the regression equation (–3700 cells per allele) is significantly different from zero. This analysis indicates that the substitution of a B allele for a D allele typically lowers the trait value in the F2 sample by 3700 Purkinje cells. A series of these types of tests are carried out at many points along each chromosome generating a profile of the strength of the statistic as a function of position—a LOD score map. The region of the chromosome in which LOD scores are within 2 LOD of the peak defines a >95% confidence interval of the QTL's position (Darvasi, 1997a). In our imaginary Purkinje cell example, the LOD score reaches a peak of 4.2 between D5Mit294 and D5Mit346. The confidence interval is about 12 cM. Figure 4, is an example of a LOD score map in which a gene that specifically modulates brain weight has been discovered on the proximal half of Chr 11. The likelihood ratio statistic (4.6 times the LOD score) is shown on the y-axis. The linkage statistic reaches a peak of 22.8 at about 12 cM. The 2-LOD confidence interval for this QTL (Bsc1 for brain size control 1) extends from 10 to 20 cM.
In practice, QTL analysis is carried out along these lines but using statistical procedures that can assess more than just the statistical strength and position of QTLs (Lynch & Walsh, 1998; Liu, 1998). Several genetic models are usually tested to assess the ways in which alleles are likely to interact with each other (linear-additive interactions, non-linear dominance interactions, and combinations of both types). More sophisticated models may also explore whether QTLs on different chromosomes interact—again linearly or non-linearly. Non-linear interactions between loci is referred to as epistasis. It is premature to worry about epistasic interactions before any QTLs have been mapped, but it is worth stressing that a realistic understanding of genetic sources of variation in CNS structure and function will ultimately demand attention to complex interactions of networks of variant gene products. Statistical criteria. What statistical criteria should be used to decide whether a QTL has been successfully mapped? Is the LOD score of 4.2 good enough? Lander and Schork (1994) deal with this issue at length and emphasize the need for stringent criteria. The main reason is that a genome-wide search of QTLs involves comparing phenotypes with many independent sets of genotypes. Remember that the gel shown in Figure 2 is just one of 50 or more gels of this type. This gel is used to test a single point in the genome (a point-wise test), but we actually test many points (or chromosomal intervals) and we are naturally much more interested in the genome-wide significance of our result. We have a classic multiple-comparisons problem, and a conventional point-wise criterion level of p = 0.05 is far too lenient. If we divide 0.05 by the 50 independent comparisons we are likely to make then we arrive at a safer estimate of the genome-wide criterion level we need to achieve with a single test. In other words, the point-wise p must to be less than 0.001 to be associated with an effective genome-wise p of less than 0.05. There has been a heated debate among quantitative geneticists regarding appropriate criteria, but there is general agreement that a QTL should not be claimed until the genome-wide significance of making a type I statistical error (an error of commission; declaring the presence of a QTL when there is really nothing there) is under 5% (Elston, 1998). Permutation tests. In our own work we use a robust non-parametric method to determine the genome-wide 5% level for each trait that we map (Churchill & Doerge, 1994). The idea behind the permutation method is simple: we randomly reassign trait values to genotypes and then we treat these permuted datasets in the same way as the original data. We then see how often QTLs are "successfully" mapped with disordered data. If many of the permuted datasets produce LOD scores that are as good or better than that generated by the correctly ordered data, then we cannot place much, if any, confidence in our putative QTL. In contrast, if fewer than 1 in 100 of the permuted datasets reaches the level of correctly ordered data, then we can be confident that the probability of having made a type I error is under 0.01. In our studies, we typically run more than 10,000 permutations, and make a histogram of the single best scores from each permutation. Using these permutation histograms we can accurately estimate the strength of association between a trait and newly discovered QTLs (Fig. B). Returning to the Purkinje cell example one last time: the permutation analysis of cell counts reveals that the probability of obtaining a LOD score of 4.2 by chance is <0.008. We can now state with reasonable certainty that there is a QTL on proximal Chr 5 that controls Purkinje cell number. In a similar way, a permuation analysis for the brain weight dataset shown in Figure 4 demonstrates that a LOD score of 4.3 (or an LRS score of 19.7) is required to reach a genome-wide p at the 0.05 level. Selective genotyping and phenotyping. The most extreme cases—those with highest and lowest trait values—are most informative for mapping QTLs (Taylor et al., 1994). These cases are more likely than others to be homozygous for alleles that increase or decrease trait values. It is therefore possible to improve the efficiency and power of detecting QTLs by initially genotyping only extreme cases. The choice of what fraction of cases to genotype depends on the relative cost of phenotyping and genotyping (Darvasi, 1997c). If phenotyping is relatively economical, one may be able to afford to generate large sets of progeny and initially genotype only 5% to 10% of cases from both tails of the distribution. In our laboratory the fraction of cases that we initially genotype is also influenced by the particular PCR and gel equipment that we use. Reactions are run in 96-well microtiter plates. We select 23 high and 22 low cases and run these with DNA from the two parental strains and the F1 hetrozygote (n = 48 samples). In this way, we are able to test two microsatellites per PCR run. Seventy markers can be analyzed in a week. Most of our F2 crosses contain 200 to 500 animals, so we are limiting our analysis to the extreme 5–10% in both tails. It is also possible to pool DNA from high and low groups and compare the relative intensity of alleles at markers that sample the entire genome (Taylor et al., 1994). When we find a chromosomal interval that harbors a suspected QTL, we then genotype all cases at these hot markers. This last step is particularly important because the initial analysis of the tails of the distribution may be influenced greatly by epistatic interactions between the main QTL and unlinked loci. Until all individuals have been typed, we will not have any good idea of the independent effects of the main QTL or of its actually chromosomal location (Darvasi, 1997c). Once a QTL has been identified the procedure can be reversed–it is now possible to save time and money by phenotyping selectively. For example, it is possible to generate a very large sample of animals, genotype DNA taken from the tips of their tails when they are still pups, and then only phenotype particular genotypes as adults. Selective procedures like this have risks because they depend on the tails of the distribution being "well behaved." But tails of distributions are often the havens of unrecognized measurement errors, developmental flukes, and as mentioned above, of rare epistatic interactions. It is also good practice to sample from both tails of the distribution. An example of the power (and risk) of selective phenotyping is an interesting study by Chorney and colleagues (1998). They report that the insulin growth factor 2 receptor (IGF2R) is a marker for very slightly higher intelligence (4 IQ points) in a mixed population of Caucasians in the Cleveland area. Their analysis is based on a comparison of allelic differences between groups of very bright children (a selection as intense as 1 in 30,000 based on test scores) and groups of normal children. There are serious interpretive difficulties related both to the intense selection of individuals more than four standard deviations away from the mean and to the intentionally unbalanced sampling design that excludes humans with low or low-normal scores. What is often not appreciated is that QTLs can have their primary effects on the variance of a trait, rather than the mean of a trait, and obviously if only one tail of a distribution is sampled one runs the risk of confounding these types of QTLs. There is therefore still no direct evidence that a QTL near IGF2R actually influences mean intelligence. A simple analysis of patterns of IGF2R alleles in a large, normally distributed, sample would resolve this issue, but indications from the within-sample correlations performed by Chorney et al., do not give any cause for optimism (r = –0.07).
The major crosses for mapping QTLs
What type of cross is best suited for different types of studies? There are currently five common types of line crosses that are commonly used to map QTLs in mice. F2 intercross progeny. The F2 intercross (described briefly in our Purkinje cell example) is currently used in the first phase of the majority of QTL studies. The advantage of this cross between lines is that it is usually possible to scan the entire genome for QTLs by typing only 70 to 90 well-spaced marker loci. This used to be a major advantage, but genotyping is getting much easier, and other factors, such as precision and power of the analysis are now more important considerations. For most purposes a group of 200 or more F2 animals will need to be generated and typed. (One person working full time can genotype approximately 200 animals at 100 marker loci in one month. You would need four 96-well thermal cyclers; each run twice a day.) The more animals one can tolerate to type, the greater the power of the analysis and the greater the number of detected QTLs (Darvasi, 1998). In general, the efficiency of phenotyping is far more critical than that of genotyping, so be sure you spend time reviewing all data collection methods from start to finish and make those changes that will allow you to generated more numbers, more accurately, more quickly. Although the F2 is a very common cross, I don't recommend it anymore. It lacks adequate positional precision. One way to improve the F2 cross without much more work is to extend the cross for two more generations, out to generation 4 (F2 to G3 to G4). This will double the precision with which QTLs are mapped. The downside is that you will need to type twice as many marker loci, as many as 200 per animal. In carrying out a four generation cross be sure NOT to mate littermates when possible. Backcross progeny. Mating F1 animals back to either or both parental strain generates one or two panels of backcross progeny. Backcross progeny are commonly used in mapping Mendelian traits, especially recessive mutations. There are only two genotype classes to contend with at any locus—the homozygote and the heterozgyote. The reduced number of genotypes simplifies scoring of genotypes and may allow QTLs to be detected more easily (Darvasi, 1998). An N2 cross may be particularly helpful in cases in which the F1 generation has an average phenotype very close to one of the parental strains; in other words, a case in which one set of parental alleles behaves in a dominant fashion. The F1 is then backcrossed to the "recessive" parental strain. The main problem with both the F2 intercross and the backcross is that QTLs usually cannot be mapped precisely. Recombination events between nearby loci will be relatively uncommon in these animals, and even with large numbers of progeny it will often be difficult to pin down a QTL to a chromosomal interval of 10 cM—roughly 20 million bp of DNA. This is a long stretch of DNA that will typically contain hundreds of genes. Fishing for good candidate genes will be tough. If we can get down to a 1–2 cM interval then we may only have to contend with a few dozen candidate genes. There are now several ways to to greatly improve the precision with which QTLs are mapped (Darvasi & Soller, 1995; Darvasi, 1997b, 1998). The most simple method is the recombinant inbred intercross method that exploits a set of more than 102 very well mapped recombinant inbred strains now available from the Jackson Laboratory (Williams et al, 2001). Advanced intercross progeny. An advanced intercross is generated by crossing F2 males and females to produce a third generation, referred to as G3 (G rather than F because filial matings are intentionally avoided). G3 individuals from different litters are then intercrossed in a way that minimizes inbreeding to produce a G4 generation (Darvasi, 1998). This process is repeated for several generations. Assuming that inbreeding can be minimized during this process, the cumulative amount of recombination between the original parental genomes doubles with each doubling of the generation number. Since all genetic maps are measured in units of recombination, not in basepairs, this process greatly increases the length of the genetic map. The consequence is a twofold improvement in the precision with which QTLs can be mapped for every twofold increase in generation number using a fixed number of offspring. Obviously, making an advanced intercross is a lot of work; in each generation 20 or more breeding cages need to be maintained (ideally 50 or more cages). The payoff is that at G8 the precision of mapping will be roughly four times greater than that of the F2 intercross. Because the genetic map is stretched so much, the number of marker loci that we need to use to scan the entire genetic map will also be increased four-fold. Each marker still only samples a region of 30 cM (the so-called swept radius), but the total length of the genome has now been stretched from 1400 cM to as much as 6000 cM. While we may have managed with 80 markers using an F2, we will need 320 markers to have the same assurance of detecting QTLs in a G8 cross. However, if we have already mapped QTLs using the F2 generation, or any of the subsequent generations, then we do not actually need to scan the entire genome of the G8 progeny. We need to remap only those chromosomal intervals that have been shown to harbor QTLs using earlier generations. The advanced intercross then can be used to map QTLs across the entire genome to a 95% confidence interval of ±2 cM. Even so this may require an analysis of 500 to 2000 cases (Darvasi, 1998). It is also practical to backcross an advanced intercross to one of the oroginal parental strains to generate an advanced backcross. The advanced backcross may have some advantages when traits are controlled by QTLs with dominant alleles or when the trait is influenced strongly by epistatic interactions. A problem with an advanced intercross is that some chromosomal intervals will drift or be selected far from the Hardy-Weinberg genotype expectation. We expect a 1:2:1 ratio of BB, BD, and DD genotypes. But if B alleles on distal Chr 1 are significantly more advantageous then D alleles for fertility and survival then by the eighth generation there may be few animals with the DD genotype. This distortion will result in non-syntenic (literally, "not on the same string or chromosome") gene loci being closely linked or associated in a statistical sense. For example two regions on Chr 1 and Chr 9 that are both enriched for the BB genotype will be in linkage disequilibrium and thus seem to be linked despite their separation on different chromosomes. If uncorrected, such non-sytenic disequilibrium will generate spurious mapping results. [A caution to anyone setting up an advanced intercross: Make sure to use as many possible parents in the penultimate generation as possible and only generate single litters from particular breeding pairs of mice. Rotate males in the the last generations rather than letting a single mating pair generate a large number of litters. Failure to rotate partners will result in marked inequities in the representation of haplotypes in the final generation used for mapping.] Recombinant inbred strains: a neuroscientist's first choice. Recombinant inbred (RI) strains are the easiest means for neuroscientists to get started mapping QTLs. They have several significant advantages, the foremost being that isolating and typing DNA is not required. RI strains are generated in the same way as an advanced intercross with the important exception that at each generation, siblings are intentionally mated (Belknap et al., 1992; Silver, 1995, p. 207–213; Williams et al., 2001). By the 20th generation, progeny are almost entirely inbred. In each of these fully inbred strains, chromosomes of the original parental strains have recombined extensively: hence the name, recombinant inbred strains. Unlike the case in the other genetic crosses we have considered, an entire strain rather than just a single mouse represents each recombinant genome. This feature is an obvious advantage for studies in which reliable neuroanatomical or behavioral traits are hard to generate from single animals. Accurate averages for each genotype can be obtained simply by phenotyping more animals. The absence of any heterozygotes also increases the phenotypic and genotypic variance for a given sample size, while at the same time reducing the number of genotype classes. This can make it easier to resolve QTLs.
The advantage of replicated recombinant genotypes. But for neuroscientists the most compelling advantage of RI strains is that it becomes possible to study relationships and correlations between many CNS traits. One can carry out immunocytochemical analyses using dozens of antibodies, then add receptor-binding studies, and finish with counts of cells using unbiased stereological methods. These structural parameters can then be compared with multiple behavioral traits (Dains et al., 1996). The accumulation of phenotypic data for these replicated genotypes, adds tremendous power to RI strains. If a QTL controls numbers of retinal ganglions, then does it also control variation in numbers of cells in the dorsal lateral geniculate nucleus, superior colliculus, or even a functionaly unrelated structure like the olfactory bulb? Do single QTLs have pleiotropic effects on multiple structures and cell populations? RI strains can be used to answer these questions. In comparison to other crosses in which each genotype is represented by a single mouse, RI strains are ideal for long-term correlative, collaborative, and corroborative studies of the genetic control of CNS structure. At present there is little information on the CNS of RI strains (Belknap et al., 1992; Dains et al.; 1996, Williams et al., 1998a). My colleague Glenn Rosen and I have begun to redress this deficiency by systematically processing brains of many of RI strains with the idea of producing a library of sectioned material to be used specifically for 3D-counting of cell populations (see <www.mbl.org>). All the tissue is embedded in celloidin, cut in coronal or horizontal planes at 30 µm, and stained with cresyl violet. The current collection consists of ~350 cases, representing more than 40 strains. If one of these recombinant inbred mice is genotyped, then the entire strain has been genotyped. For this reason, genotype data also accumulates as more researchers type these strains. We maintain a large database of error-checked and curated genotypes for five of the most common RI sets (AXB, BXA, BXD, BXH, and CXB). One of the largest and best-characterized RI sets consists of 35 BXD strains generated by Benjamin Taylor of the Jackson Laboratory by crossing C57BL/6J to DBA/2J (Taylor, 1989). Over 1750 gene and marker loci have now been genotyped in the majority of these strains. To map a QTL using these RI strains, we simply phenotype a sample from each of the 35 strains and then compare the pattern of strain averages or residuals with the distribution pattern of alleles at a subset of approximately 1000 loci. The procedure is explained in detail in Williams et al. (1998a) and complete genotype databases for BXD and other RI strains are available at www.nervenet.org. One last advantage of RI strains is that the genetic maps have a resolution that is 4-fold greater than that in an F2 cross. Like maps of an advanced intercross, those of RI strains are expanded, and in some cases it is possible to map a QTL with a precision of ± 2 cM (Williams et al., 1998a; Williams et al., 2001). This also means that QTLs mapped with RI strains will usually be associated with single genes, rather than sets of linked genes. The main disadvantage of RI strains. At present the major disadvantage of RI strains is that there are still too few of them, and as a result only QTLs that have comparatively large effects can be mapped. This is not a serious problem at an early stage of analysis, before any QTLs have been mapped. In our work we have consistently been able to use the BXD strains to map at least one QTL controlling each of the following traits: ganglion cell number, eye size, brain weight, and cerebellar weight. But there are many other QTLs controlling each of these traits, and mapping QTLs with less robust effects will usually require larger numbers of recombinant genotypes. This has usually involved a second phase in which N2, F2 or advanced intercross progeny are used to confirm and extend the genetic analysis. To provide a better solution we have recently genotyped a set of 100 RI strains that all share one common parent (C57BL/6J). It is straightforward to pool data from multiple RI sets and to statistically assemble an RI super set to improve statistical power. Combining data from several sets of RI strains should double or triple the yield of QTLs. Another reported disadvantage of RI strains is that gene dominance effects can not be assayed since all of the RI strains are fully inbred. The absense of heterozygotes prevents one from determining the effects of a single allele on a trait. However, this is a trivial problem to overcome since it is easy to generate F1 intercrosses between RI strains and thereby make large numbers of obligate heterozygotes on any interval desired. Congenic strains. Congenic strains are generated by crossing two inbred strains (generating an F1 hybrid) and then backcrossing repeatedly to one parental strains (Morel et al., 1997; Wakeland et al., 1997). The idea is to transfer and isolate a specific chromosomal interval from one strain (the donor) to another strain (the recipient). For example, we might wish to transfer an allele that is associated with a low Purkinje cell population from the genome of C57BL/6 onto the DBA/2J strain. To do this we would backcross the F1 progeny to DBA/2J. The backcross progeny—refered to as the N2 progeny—must then be genotyped at markers on both sides of the QTL and perhaps one additional marker half way between. (If the QTL is poorly localized three or even more markers may need to be typed to insure that the entire interval that may harbor the QTL is heterozygous in animals chosen for breeding.) On average 50% of the genome of the N2 progeny will be homozygous for DBA/2 alleles. Animals that have inherited one B allele at both markers M1 and M2 (Fig. 2) are then crossed back to the DBA/2 parental strain again. In this N3 backcross generation 75% of the genome will be homozygous for the DBA/2 genotype, but because we intentionally bred animals that were heterozygotes between M1 and M2, an average of half of the N3 progeny will still be heterozygous in this interval. The process of genotyping a few specific markers in a small number of progeny and then crossing mice that carry B alleles back to DBA/2 is repeated for eight or more generations. Homozygosity for DBA/2 alleles increases from 75% at N3, to 87.5% at N4, and to 99.8% at N10. N10 progeny that are heterozygous for markers M1 and M2 are mated. Some of their offspring will be homozygous for C57 alleles in the M1–M2 interval and these mice and their offspring are used produce a constant stream of congenic animals that are homozygous for the C57 allele of our Purkinje cell QTL, but which are otherwise almost entirely DBA/2 type. We have transferred the low allele from one strain to another. We should probably also transfer the high Purkinje cell allele from DBA/2 to C57BL/6, generating what is called the reciprocal congenic strain. We have in essence turned a complex polygenic trait into a more tractable single gene trait. Now it is possible to phenotype many of these reciprocal congenic mice and compare Purkinje cells populations. Differences are due to the QTL in the M1–M2 interval. We can do this at any stage of development to determine when and where the allelic differences begins to affect Purkinje cell proliferation or survival. Congenic strains are presently the main tool used to fine-map QTLs. This is accomplished by making sets of strains that are congenic for overlapping intervals that collectively define intervals that can be as short as 1 cM across the QTL's presumed location. Phenotypes of congenic strains are compared, and those that differ from parental strains are presumed to harbor the QTL (Darvasi, 1997b). Once a QTL has been mapped to this level of precision it become feasible to test candidate genes that map to the 2-LOD confidence interval. There can be problems with a congenic approach to mapping QTLs. The primary problem is that as a QTL is introgressed into a recipient strain, it may lose its effects on phenotypes. To minimize frustration, the phenotype should be monitored during the process of introgressing the QTL (see Vadasz et al., 1998 for a beautiful example). QTLs can evaporate because key epistatic interactions upon which a phenotype depends are lost. In this predicament, it may be possible to identify and conserve intervals that appear to be critical for the penetrance of the QTL's effects. Recombinant inbred intercross (RIX) progeny. This powerful yet simple QTL mapping method was devised by David Threadgill and colleagues and involves generating all or a subset of the many pairs of intercrosses (hence RIXs) between a set of recombinant inbred strains (Williams et al 2000). The derived RIX set extends the number of genomes available for phenotyping by a factor of n(n-1)/2, where n is the number of original RI strains. For example, the 13 CXB/By strains and the 35 BXD/Ty that have been used heavily can be supplemented by 6 and 17 times as many novel recombinant RIX genotypes, respectively. Each individual RIX strain has a unique but entirely predictable genome and like RI strains, many genetically defined RIX individuals can be phenotyped to greatly improve trait reliability. However, unlike an RI set, an RIX set closely resembles an F2 intercross, with a 1:2:1 segregation ratio of genotypes at marker loci. Furthermore, none of the RIX progeny are inbred, resulting in more robust mice from which more reliable traits can be extracted. Parental effects can be controlled to some extent by changing the polarity of the RIX; in other words, the maternal and paternal strains can be switched to produce reciprocal RIX progeny which are genetically identical. Any significant differences between these reciprocal crosses are due to parental effects. The statistical properties of RIX sets, that is, their power to detect QTLs, the positional precision of mapping data, and the accuracy of estimates of allelic effects of the trait of interest, are significantly better than those of the original RI set. For example, the statistical power of a complete RIX set (n = 561 RIXs) derived from the 34 BXD/Ty RI strains will typically be boosted 4- to 6-fold. QTLs that control as little as 5% of the phenotypic variance will often be detected with a power of better than 0.8. The 2-LOD confidence interval will also be somewhat smaller. Given the already extensive phenotypic data for RI strains of mice, the RIX method provides a highly effective means to confirm and extend existing QTL mapping data. And no genotyping is required! Selective analysis of specific RIX strains can also be a powerful method to test models of gene action and interaction effects among multiple QTLs. For an example of the application of this method see our recent abstract (Williams et al., 2000). Like the other crosses, there are drawbacks to the RIX approach. The current problem with RIX mapping is that non-syntenic associations, that is, statistical linkage between different chromosomal segments, can be high. This problemin was already eluded to in the context of RI mapping (and see Williams et al., 2001), but in RIX mapping this problem has more obvious effects and will generate spurious QTLs. To exploit RIX mapping effectively will require carefully contructed RIX panels in which non-sytenic association has been controlled either by selection or by sophisticated statistical control. Combining results from two or more mapping studies. It is not difficult to perform a meta-analysis of multile independent sets of mapping results using a method explained in Sokal and Rohlf (1996, section 18.1). In brief, one computes the combined probabilities of linkage in a number of crosses. This method was used to help map the Nnc1 locus (Williams et al., 1998, see equation in the methods) by combining data from two sets of RI strains, BXD and BXH. The same method can be used to combine an apparent hodge-podge of RI, F2, and N2 and advanced intercross data sets. This is most productive when the same sets of alleles are segregating in the different crosses (i.e., BXD, B6D2F2), but can even work in crosses that do not share the same parental genomes. The main difficulty in applying this method is deciding what values to actually combine. We have settled on a simple procedure in which all markers used in each cross are assigned a single "genome-wide" position value. These values have units of Morgans, and the range of values extends from 0.00 for the most centromeric marker on Chr 1 to 15.9 for the distal-most marker on Chr X. These uniform genome-position values provide a common framework map for every cross. The point-wise P values are computed for all markers, and values between markers are interpolated in 1 cM bins. The P values of identical 1 cM bins are then combined. This pooling procedure (BXD plus and F2) was essential in mapping the first set of QTLs affecting olfactory bulb weight (Williams et al., 2001). (This paragraph added Oct 27, 2000 by RW)
The highs and lows of QTL analysis
QTL mapping is initially done at a level of analysis that is far removed from cellular and molecular mechanisms, and it may at times seem that the research has lost touch with biology. But keep in mind that this QTL analysis is itself just a prelude to a renewed molecular and cellular analysis—that the first aim is simply to determine where key regulatory genes are located. In some ways this first stage is like air reconnaissance: At high altitude, we hope to succeed in discerning the outlines of roads and walls marking lost cities in the desert. We now know the approximate locations, but we need to get on the ground to explore, to survey, and ultimately, to excavate these sites. The payoff can be great, and in QTL analysis the exploration on the ground does not need to be delayed for long. As soon as QTLs have been mapped, and long before candidate genes have been identified or cloned, QTLs can be used as "reagents" to probe neuronal development and function. In our own work on neuron number control 1 (Nnc1)—a QTL that has pronounced effects on numbers of retinal ganglion cell populations—Richelle Strom and I have been able to show that this QTL modulates neurogenesis rather than cell death (Strom & Williams, 1999). We now also suspect that Nnc1 may be the thyroid hormone alpha receptor gene, and in collaboration with Guomin Zhou, Douglas Forrest, and Bjorn Vennström, we are now examining effects of inactivating this gene on the ganglion cell population. There are several other powerful ways to exploit QTLs prior to cloning. Chromosomal segments containing QTL alleles associated with high or low phenotypes can be transferred to well-characterized inbred strains of mice—producing the congenic strains mentioned above (Darvasi, 1997b). Once a set of congenic mice has been generated, it becomes possible to explore developmental, pathological, and even environmental mechanisms that lead to differences between strains that carry the alleles associated with high and low traits. Furthermore, sets of high and low alleles at genes on different chromosomes can be combined in different combinations to test how QTLs interact to modify CNS architecture. The near future of QTL mapping. The principal goal of QTL analysis is to identify the polymorphic sequences associated with each QTL. As the genomes of both humans and mice are sequenced in the next decade, the still arduous process of identifying genes will become progressively easier. We can soon expect to have detailed maps and databases of genes expressed in different tissue and cell types at different stages of development. It will then be possible to combine data on well-mapped QTLs with precise data on chromosomal positions of particular types of genes and expressed sequence tags (ESTs) to quickly winnow the list of candidate genes. This future belongs to those who start weighing, counting, measuring, and mapping now.
Acknowledgments
This work was supported in part by grants from the NEI (EY08868 and EY6627) and NINDS (NS35485) to RW. I thank Dr. Benjamin Taylor, James Cheverud, Ty Vaughn, and Robert Hitzeman for corrections and comments. I thank my colleagues Drs. Guomin Zhou, Richelle Strom, David Airey, and Glenn Rosen for their help. My thanks to Kathryn Graehl for editing, Alexander Williams for building internet sites, and to Drs. John Morrison and Patrick Hof for organizing the 1998 Short Course in Quantitative Neuroanatomy.
Literature Cited
Abercrombie M (1946) Estimation of nuclear population from microtome sections. Anat. Rec. 94:239-247.http://www.nervenet.org/papers/Aberfp.html Airey DC, Lu l, Williams RW (2001) Genetic control of the mouse cerebellum: Identification of quantitative trait loci modulating size and architecture. J Neurosci. in review.http://www.nervenet.org/papers/cerebellum2000.html Aylsworth, AS (1998) Defining disease phenotypes. In: Approaches to gene mapping in complex human diseases. Haines JL, Pericak-Vance MA, eds. Wiley-Liss, pp 53–76. Belknap JK, Phillips TJ, O'Toole LA (1992) Quantitative trait loci associated with brain weight in the BXD/Ty recombinant inbred mouse strains. Brain Res Bull 29:337–344. Buck KJ, Metten P, Belknap JK, Crabbe JC (1997) Quantitative trait loci involved in genetic predisposition to acute alcohol withdrawal in mice. J Neurosci 17:3946–3955.http://www.jneurosci.org/cgi/content/full/17/10/3946 Chorney MJ, Chorney K, Seese N, Owen MJ, Daniels J, McGuffin P, Thompson LA, Detterman DK, Benbow C, Eley T, Plomin R (1998) A quantitative trait locus associated with cognitive ability in children. Psychological Rev 9:159–166. Churchill GA, Doerge RW (1994) Empirical threshold values for quantitative trait mapping. Genetics 138:963–971. Crawley JN, Belknap JK, Collins A, Crabbe JC, Frankel W, Henderson N, Hitzemann RJ, Maxson SC, Miner LL, Silva AJ, Wehner JM, Wynshaw-Brois A, Paylor R (1997) Behavioral phenotypes of inbred mouse strains: implications and recommendations for molecular studies. Psychopharmacol 132:107–124. Dains K, Hitzeman B, Hitzeman R (1996) Genetic, neuroleptic-response and the organization of cholinergic neurons in the mouse striatum. J Pharmacol Exp Ther 279:1430–1438. Darvasi A, Soller M (1995) Advanced intercross lines, an experimental population for fine genetic mapping. Genetics 141:1199–1207. Darvasi A (1997a) Behav Genet 27:125–132. Darvasi A (1997b) Interval-specific congenic strains (ISCS): an experimental design for mapping a QTL into a 1-centimorgan interval. Mamm Gen 8:163–167. Darvasi A (1997c) The effect of selective genotyping on QTL mapping accuracy. Mamm Gen 8:67–68. Darvasi A (1998) Experimental strategies for the genetic dissection of complex traits in animal models. Nat Gen 18:19–24. Dietrich W, Katz H, Lincoln SE, Shin HS, Friedman J, Dracopoli NC, Lander ES (1992) A genetic map of the mouse suitable for typing intraspecific crosses. Genetics 131:423–447. Dietrich W, Miller JC, Steen RG, Merchant M, Damron D, Nahf R, Gross, A, Joyce DA, Wessle M, Dredge RD, Marquis A, Stein LD, Goodman N, Rage DC, Lander ES (1994) A genetic map of the mouse with 4,006 simple sequence length polymorphisms. Nature Gen 7:220–245. Elston RC (1998) Methods of linkage analysis—and the assumptions underlying them. Am J Hum Genet 63:931–934. Avaiable at <http://www.journals.uchicago.edu/AJHG/journal/issues/v63n4/980636/980636.html>. Falconer DS, Mackay TFC (1996) Introduction to quantitative genetics. 4th ed. Longman Scientific, Harlow, Essex. Gilissen E, Zilles K (1996) The calcarine sulcus as an estimate of the total volume of the human striate cortex: a morphometric study of reliability and intersubject variability. J Brain Res 37:57–66. Greenspan RJ (2001) The flexible genome. Nature Reviews 2:383–387. Gundersen HJG, Bagger P, Bendtsen TF, Evans SM, Korbo L, Marcussen N, Møller A, Nielsen K, Nyengaard JR, Pakkenberrg P, Sørensen FB, Vesterby A, West MJ (1988) The new stereological tools: disector, fractionator, nucleator, and point sampled intercepts and their use in pathological research and diagnosis. Acta Path Microbiol Immunol Scand 96: 857-881. Hegmann JP, Possidente B (1981) Estimating genetic correlations from inbred strains. Behav Gene 11:103–114. Kearsey MJ, Pooni HS (1996) The genetical analysis of quantitative traits. Chapman Hall, London. Laird PW, Zijderbeld A, Linders K, Rudnicki MA, Jaenisch R, Berns A (1991) Simplified mammalian DNA isolation procedure. Nucleic Acid Res 19:4293. Lander ES, Botstein D (1989) Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121:185–199. Lander ES, Schork NJ (1994) Genetic dissection of complex traits. Science 265:2037–2048. Lu L, Airey DC, Williams RW (2001) Genetic dissection of the mouse hippocampus: Identification of loci with specific effects on hippocampal size. Journal of Neurosicence 21:3503–3514. JN 0625-00. Lui BH (1998) Statistical genomics. Linkage, mapping and QTL analysis. CRC Press, Boca Raton FL. Lynch M, Walsh B (1998) Genetics and analysis of quantitative traits. Sinauer, Sunderland MA. Manly K (1993) A Macintosh program for storage and analysis of experimental genetic mapping data. Mamm Genome, 4: 303–313. Morel L, Mohan C, Yu Y, Croker BP, Tian N, Deng A, Wakeland EK (1997) Functional dissection of systemic lupus erthematosus using congenic mouse strains. J Immuno 158:6019–6028. Ott J, Hoh J (2000) Statistical approaches to gene mapping. Am J Hum Genet 67:289–294. Pennisi E (2000) Mouse sequencers take up the shotgun. Science 287:1179–1181. Roff DA (1997) Evolutionary quantitative genetics. Chapman & Hall, New York. Rosen GD, Williams RW (2001) Complex trait analysis of the mouse striatum: Independent QTLs modulate volume and neuron number. BMC Neuroscience 2:5 @ www.biomedcentral.com/1471-2202/2/5 Sandberg R, Yasuda R, Pankratz DG, Carter TA, Del Rio JO, Wodicka L, Mayford M, Lockhart DJ, Barlow C (2000) Regional and strain-specific gene expression mapping in the adult mouse brain. Proc Natl Acad Sci USA 97: 11039–11043. Silver LM (1995) Mouse genetics: Concepts and applications. Oxford UP, New York. Sokal RR, Rohlf FJ (1995) Biometry: the principels and practice of statistics in biological research, 3rd ed. Freeman and Co, San Francisco. Suner I, Rakic P (1996) Numerical relationship between neurons in the lateral geniculate nucleus and primary visual cortex in adult macaque monkeys. Vis Neurosci 13:585–590. Strom RC, Williams RW (1998) Roles of cell production and cell death in the generation of normal variation in neuron number. J Neurosci 18:9948–9953. http://www.nervenet.org/papers/dev.html. Takahashi JS, Pinto LH, Vitaterna MH (1994) Forward and reverse genetic approaches to behavior in the mouse. Science 264:1724–1733. Tanksley SD (1993) Mapping polygenes. Annu Rev Genet 27:205–233. Taylor BA (1989) Recombinant inbred strains. In: Genetic variants and strains of laboratory mouse. 2nd ed. pp 773–789. Oxford UP, New York. Taylor BA (1972) Genetic relationships between inbred strains of mice. J. Heredity 63:83–86. Taylor BA, Navin A, Phillips SJ (1994) PCR-amplification of simple sequence repeat variants from pooled DNA samples for rapidly mapping new mutations of the mouse. Genomics 21:626–632. Vadasz C, Sziraki I, Sasvari M, Kabai P, Murthy LR, Saito M, Laszlovszky I (1998) Neurochemical Res 23:1337–1354. Wakeland E, Morel L, Achey K, Yui M, Longmate J (1997) Speed congenics: a classic technique in the fast lane (relatively speaking). Immunology Today 18:472–477. Weiss KM, Terwilliger JD (2000) How many diseases does it take to map a gene with SNPs? Nature Genetics 26:151–157. Williams RW (2000) Mapping genes that modulate mouse brain development: a quantitative genetic approach. In: Mouse Brain Development (Goffinet AF, Rakic P, eds). Springer, New York, pp 21–49. Full text and figures available at http://www.nervenet.org/papers/BrainRev99.html. Williams RW, Rakic P (1988) Three-dimensional counting: An accurate and direct method to estimate numbers of cells in sectioned material. J Comp Neurol 278:344–353. Full text with corrections and additions at http://www.nervenet.org/papers/3DCounting.html Williams RW, Strom RC, Rice DS, Goldowitz D (1996) Genetic and environmental control of variation in retinal ganglion cell number in mice. J Neurosci 16:7193–7205.http://www.jneurosci.org/cgi/content/full/16/22/7193 Williams RW, Strom RC, Goldowitz D (1997) Soc Neurosci Abst Williams RW, Strom RC, Goldowitz D (1998a) Natural variation in neuron number in mice is linked to a major quantitative trait locus on Chr 11. J Neurosci 18:138–146.http://www.jneurosci.org/cgi/content/full/18/1/138 Williams RW, Strom RC, Zhou G, Yan Z (1998b) Genetic dissection of retinal development. Sem Cell Devel Biol: in press. http://www.nervenet.org/papers/Retina_Rev.html Williams RW, Gu J, Qi S, Lu L (2001). The genetic structure of recombinant inbred mice: high-resolution consensus maps for complex trait analysis. Release 1, January 15, 20001 at nervenet.org/papers/bxn.html. Genome Biology, in review. Wimer RE, Wimer CC (1989) On the sources of strain and sex differences in granule cell number in the dentate area of house mice. Dev Brain Res 48:167–176. Zhou G, Williams RW (1997) Mapping genes that control variation in eye weight, retinal area, and retinal cell density. Soc Neurosci Abst 23:864. http://www.nervenet.org/papers/ZhouSN98.html
Copyright © 1998 by R.W. Williams
|
Neurogenetics at University of Tennessee Health Science Center
| Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org